
 的距离比M到定直线l:x=-p的距离小
的距离比M到定直线l:x=-p的距离小 .
. ,求△AOB面积的最小值;
,求△AOB面积的最小值; 对称?若存在,求出直线m的方程,若不存在,说明理由.
对称?若存在,求出直线m的方程,若不存在,说明理由.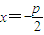 的距离相等,点M的轨迹为抛物线,由此可求出轨迹C的方程.
的距离相等,点M的轨迹为抛物线,由此可求出轨迹C的方程.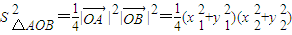 =
=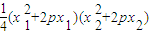 =16p4,由此导出△AOB面积最小值为4p2.
=16p4,由此导出△AOB面积最小值为4p2.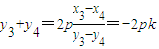 ,y=-pk,再由D(x,y)在
,y=-pk,再由D(x,y)在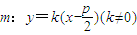 上,知点D(x,y)在抛物线外,所以在轨迹C上不存在两点P,Q关于直线m对称.
上,知点D(x,y)在抛物线外,所以在轨迹C上不存在两点P,Q关于直线m对称. 的距离相等
的距离相等

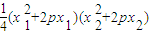
 ≥
≥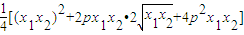 =16p4
=16p4
 上
上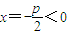 ,点D(x,y)在抛物线外
,点D(x,y)在抛物线外

科目:高中数学 来源: 题型:
| p |
| 2 |
| p |
| 2 |
| OA |
| OB |
| p |
| 2 |
查看答案和解析>>
科目:高中数学 来源:宣武区二模 题型:解答题
| p |
| 2 |
| p |
| 2 |
| OA |
| OB |
| p |
| 2 |
查看答案和解析>>
科目:高中数学 来源:《第2章 圆锥曲线与方程》2010年单元测试卷(1)(解析版) 题型:解答题
 的距离比M到定直线l:x=-p的距离小
的距离比M到定直线l:x=-p的距离小 .
. ,求△AOB面积的最小值;
,求△AOB面积的最小值; 对称?若存在,求出直线m的方程,若不存在,说明理由.
对称?若存在,求出直线m的方程,若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:2010年北京市宣武区高考数学二模试卷(理科)(解析版) 题型:解答题
 的距离比M到定直线l:x=-p的距离小
的距离比M到定直线l:x=-p的距离小 .
. ,求△AOB面积的最小值;
,求△AOB面积的最小值; 对称?若存在,求出直线m的方程,若不存在,说明理由.
对称?若存在,求出直线m的方程,若不存在,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com