
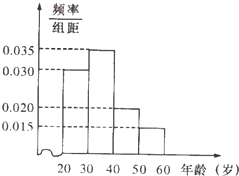
 ij������120�����ˣ������䶼��20��60��֮�䣬�������������[20��30����[30��40����[40��50����[50��60���ֳ����飬��Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������Ϊ�˿����²�Ʒ���������µ������豸��Ҫ��ÿ�����˶�Ҫ�μ�A��B������ѵ����ѵ��������н�ҵ���ԣ���֪�������������ѵ��ҵ���Գɼ���������������ʾ������������ѵ��������ģ���ҵ����Ҳ����Ӱ�죮
ij������120�����ˣ������䶼��20��60��֮�䣬�������������[20��30����[30��40����[40��50����[50��60���ֳ����飬��Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������Ϊ�˿����²�Ʒ���������µ������豸��Ҫ��ÿ�����˶�Ҫ�μ�A��B������ѵ����ѵ��������н�ҵ���ԣ���֪�������������ѵ��ҵ���Գɼ���������������ʾ������������ѵ��������ģ���ҵ����Ҳ����Ӱ�죮| ������� | A����ѵ�ɼ��������� | B����ѵ�ɼ��������� |
| [20��30�� | 27 | 16 |
| [30��40�� | 28 | 18 |
| [40��50�� | 26 | 9 |
| [50��60] | 6 | 4 |
���� ��1����Ƶ�ʷֲ�ֱ��ͼ��֪�������[20��30����[30��40����[40��50����[50��60]��������Ƶ�ʷֱ�Ϊ0.3��0.35��0.2��0.15���ɴ���ʾ���ĸ�����ηֱ�Ӧ��ȡ��������
��2������������е�ֵ�ֱ�Ϊ25��35��45��55����Ӧ��Ƶ�ʷֱ�Ϊ0.3��0.35��0.2��0.15���ɴ����ɴ˹���ȫ�����˵�ƽ�����䣮
��3����Ϊ�����[20��30���Ĺ�����Ϊ36���Ӹ��������ȡ1�ˣ�A��B������ѵ��ҵ���Գɼ�������ĸ���Ϊ$\frac{1}{3}$�������[40��50���Ĺ�����Ϊ24���Ӹ��������ȡ1�ˣ�A��B������ѵ��ҵ���Գɼ�������ĸ���Ϊ$\frac{1}{4}$�������裬X�Ŀ���ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к���ѧ������
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ��֪�������[20��30����[30��40����[40��50����[50��60]��������Ƶ�ʷֱ�Ϊ0.3��0.35��0.2��0.15��
��Ϊ40��0.3=12��40��0.35=14��40��0.2=8��40��0.15=6��
���������[20��30����[30��40����[40��50����[50��60��Ӧ��ȡ�������ֱ�Ϊ12��14��8��6��
��2����Ϊ����������е�ֵ�ֱ�Ϊ25��35��45��55��
��Ӧ��Ƶ�ʷֱ�Ϊ0.3��0.35��0.2��0.15��
��$\overline{x}$=25��0.3+35��0.35+45��0.2+55��0.15=37��
�ɴ˹���ȫ�����˵�ƽ������ԼΪ37��
��3����Ϊ�����[20��30���Ĺ�����Ϊ120��0.3=36��
�Ӹ��������ȡ1�ˣ��ɱ�֪������A����ѵ��ҵ���Գɼ�����ĸ���Ϊ$\frac{27}{36}$=$\frac{3}{4}$��
B����ѵ��ҵ���Գɼ�����ĸ���Ϊ$\frac{16}{36}=\frac{4}{9}$��
����A��B������ѵ��ҵ���Գɼ�������ĸ���Ϊ$\frac{3}{4}��\frac{4}{9}=\frac{1}{3}$��
��Ϊ�����[40��50���Ĺ�����Ϊ120��0.2=24��
�Ӹ��������ȡ1�ˣ��ɱ�֪������A����ѵ��ҵ���Գɼ�����ĸ���Ϊ$\frac{16}{24}$=$\frac{2}{3}$��
B����ѵ��ҵ���Գɼ�����ĸ���Ϊ$\frac{9}{24}=\frac{3}{8}$��
����A��B������ѵ��ҵ���Գɼ�������ĸ���Ϊ$\frac{2}{3}��\frac{3}{8}=\frac{1}{4}$��
�����裬X�Ŀ���ȡֵΪ0��1��2��
P��X=0��=��1-$\frac{1}{3}$����1-$\frac{1}{4}$��=$\frac{1}{2}$��
P��X=1��=$\frac{1}{3}����1-\frac{1}{4}��+��1-\frac{1}{3}����\frac{1}{4}=\frac{5}{12}$��
P��X=2��=$\frac{1}{3}��\frac{1}{4}=\frac{1}{12}$��
����X�ķֲ�����
| X | 0 | 1 | 2 |
| P | $\frac{1}{2}$ | $\frac{5}{12}$ | $\frac{1}{12}$ |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ������������߿��ж��DZؿ�����֮һ��


 �������Ͽ��㱾ϵ�д�
�������Ͽ��㱾ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=$��\frac{5}{4}$x | B�� | y=$��\frac{4}{5}$x | C�� | y=$��\frac{16}{25}$x | D�� | y=��$\frac{25}{16}$x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ����������� | ||
| C�� | ��Ҫ���� | D�� | ���϶����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 24 | B�� | 16 | C�� | 12 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com