
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 是过点
是过点![]() ,倾斜角为
,倾斜角为![]() 的直线,以直角坐标系
的直线,以直角坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅰ)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的一个参数方程;
的一个参数方程;
(Ⅱ)曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】在一次摸取奖票的活动中,已知中奖的概率为![]() ,若票仓中有足够多的票则下列说法正确的是
,若票仓中有足够多的票则下列说法正确的是![]()
![]()
A. 若只摸取一张票,则中奖的概率为![]()
B. 若只摸取一张票,则中奖的概率为![]()
C. 若100个人按先后顺序每人摸取1张票则一定有2人中奖
D. 若100个人按先后顺序每人摸取1张票,则第一个摸票的人中奖概率最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】滕州市教育局为了解学生网络教学期间的学习情况,从初中及高中共抽取了50名学生,对他们每天平均学习时间进行统计.请根据下面的各班人数统计表和学习时间的频率分布直方图解决下列问题:
年级 | 人数 |
初一 | 4 |
初二 | 4 |
初三 | 6 |
高一 | 12 |
高二 | 6 |
高三 | 18 |
合计 | 50 |

(1)抽查的50人中,每天平均学习时间为6~8小时的人数有多少?
(2)经调查,每天平均学习时间不少于6小时的学生均来自高中.现采用分层抽样的方法,从学习时间不少于6小时的学生中随机抽取6名学生进行问卷调查,求这三个年级各抽取了多少名学生;
(3)在(2)抽取的6名学生中随机选取2人进行访谈,求这2名学生来自不同年级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱![]() 的侧棱与底面垂直,
的侧棱与底面垂直,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,且
上,且![]() .
.

(Ⅰ)证明:无论![]() 取何值,总有
取何值,总有![]() ;
;
(Ⅱ)当![]() 取何值时,直线
取何值时,直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 最大?并求该角取最大值时的正切值.
最大?并求该角取最大值时的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶甲、乙两个村各50户贫困户.为了做到精准帮扶,工作组对这100户村民的年收入情况、劳动能力情况、子女受教育情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标![]() 和
和![]() ,制成下图,其中“
,制成下图,其中“![]() ”表示甲村贫困户,“
”表示甲村贫困户,“![]() ”表示乙村贫困户.
”表示乙村贫困户.
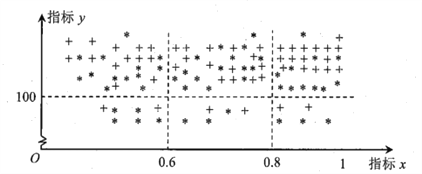
若![]() ,则认定该户为“绝对贫困户”,若
,则认定该户为“绝对贫困户”,若![]() ,则认定该户为“相对贫困户”,若
,则认定该户为“相对贫困户”,若![]() ,则认定该户为“低收入户”;
,则认定该户为“低收入户”;
若![]() ,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
(1)从甲村50户中随机选出一户,求该户为“今年不能脱贫的绝对贫困户”的概率;
(2)若从所有“今年不能脱贫的非绝对贫困户”中选3户,用![]() 表示所选3户中乙村的户数,求
表示所选3户中乙村的户数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(3)试比较这100户中,甲、乙两村指标![]() 的方差的大小(只需写出结论).
的方差的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如下,已知分数在100~110的学生数有21人。

(Ⅰ)求总人数N和分数在110~115分的人数n;
(Ⅱ)现准备从分数在110~115分的n名学生(女生占![]() )中任选2人,求其中恰好含有一名女生的概率;
)中任选2人,求其中恰好含有一名女生的概率;
(Ⅲ)为了分析某个学生的学习状态,对其下一阶段的学习提供指导性建议,对他前7次考试的数学成绩x(满分150分),物理成绩y进行分析,下面是该生7次考试的成绩。
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩y与数学成绩x是线性相关的,若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据![]() 其回归线
其回归线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com