练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】对于函数，若在定义域内存在实数，满足，则称为“局部奇函数”．

    为定义在上的“局部奇函数”；

    曲线与轴交于不同的两点；

    若为假命题， 为真命题，求的取值范围．

    【答案】或或

    【解析】试题分析：首先根据已知条件并结合换元法和二次函数在区间上的最值以及一元二次方程根的情况分别求出命题， 为真命题时所满足的的取值范围，然后根据已知条件可知命题， 中一个为真命题，一个为假命题，并利用补集的思想求出的取值范围.

    试题解析：若p为真，则由于为的局部奇函数，从而，即在上有解，令，则，又在上递减，在上递增，从而，得，故有. 若为真，则有，得或. 又由“”为假命题，“”为真命题，则与一真一假；若真假，则，得无交集；若假真，则，得或或，综上知的取值范围为或或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某单位共有老、中、青职工430人,其中青年职工160人，中年职工人数是老年职工人数的2倍。为了解职工身体状况，现采用分层抽样方法进行调查，在抽取的样本中有青年职工32人，则该样本中的老年职工人数为

    A. 9 B. 18 C. 27 D. 36

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在研究色盲与性别的关系调查中，调查了男性480人，其中有38人患色盲，调查的520个女性中6人患色盲．　

    （Ⅰ）根据题中数据建立一个的列联表；

    （Ⅱ）在犯错误的概率不超过0.001的前提下，能否认为“性别与患色盲有关系”？

    附：参考公式，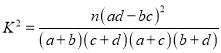

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在透明塑料制成的长方体容器内灌进一些水（未满），现将容器底面一边固定在底面上，再将容器倾斜，随着倾斜度的不同，有下列四种说法：

    ①水的部分始终呈棱柱状；

    ②水面四边形的面积为定值；

    ③棱始终与水面平行；

    ④若， ，则是定值.

    则其中正确命题的个数的是（ ）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列满足．

    （1）求；

    （2）求的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

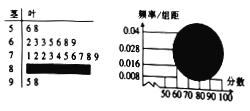
    【题目】如图，某校高一（1）班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分，据此解答如下问题：

    （1）求该班全体男生的人数及分数在之间的男生人数；

    （2）根据频率分布直方图，估计该班全体男生的数学平均成绩（同一组中的数据用该组区间的中点值代表）；

    （3）从分数在中抽取两个男生，求抽取的两男生分别来自、的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （1）当时，求函数的单调区间；

    （2）若关于的不等式在上有解，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， .

    （Ⅰ）若是奇函数，且在区间上是增函数，求的值；

    （Ⅱ）设，若在区间内有两个不同的零点， ，求的取值范围，并求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设方程有两个不等的负根， 方程无实根，若“”为真，“”为假，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案