
分析 (I)由题意可得f(x)max≤1,)由||x-2a|-|x-5||≤|(x-2a)-(x-5)|=|2a-5|,可得f(x)的最大值,再由绝对值不等式的解法可得a的范围;
(Ⅱ)运用对数函数的性质,可得loga(1-b)<0,loga(1+b)>0,将绝对值去掉,再由作差比较法,即可得证.
解答 解:(I)f(x)=|x-2a|-|x-5|,且对于任意x∈R都有f(x)≤1恒成立,
即为f(x)max≤1,
由|f(x)|=||x-2a|-|x-5||≤|(x-2a)-(x-5)|=|2a-5|,
当(x-2a)(x-5)≥0时,取得最大值|2a-5|,
即有|2a-5|≤1,
解得2≤a≤3,
即有a的范围是[2,3]:
(Ⅱ)证明:由0<b<1,可得0<1-b<1,1<1+b<2,
又2≤a≤3,
可得loga(1-b)<0,loga(1+b)>0,
|loga(1-b)|-|loga(1+b)|=-loga(1-b)-loga(1+b)
=-loga(1-b2),
由0<b<1可得,0<1-b2<1,即有loga(1-b2)<0,
则|loga(1-b)|-|loga(1+b)|>0,
即为|loga(1-b)|>|loga(1+b)|.
点评 本题考查不等式恒成立问题的解法,注意运用绝对值不等式的性质,考查对数不等式的证明,注意运用对数函数的性质,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
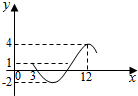
| A. | $\frac{2π+3}{3}$ | B. | $\frac{π+2}{2}$ | C. | $\frac{π+3}{3}$ | D. | π+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
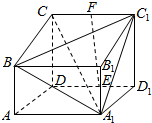 如图,四棱柱ABCD-A1B1C1D1中,侧面AA1D1D为矩形,AB⊥平面AA1D1D,CD⊥平面AA1D1D,E、F分别为A1B1、CC1的中点,且AA1=CD=2,AB=AD=1.
如图,四棱柱ABCD-A1B1C1D1中,侧面AA1D1D为矩形,AB⊥平面AA1D1D,CD⊥平面AA1D1D,E、F分别为A1B1、CC1的中点,且AA1=CD=2,AB=AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 原点在圆内 | B. | 原点在圆上 | C. | 原点在圆外 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当a>0时,函数F(x)有2个零点 | B. | 当a>0时,函数F(x)有4个零点 | ||
| C. | 当a<0时,函数F(x)有2个零点 | D. | 当a<0时,函数F(x)有3个零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com