
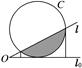
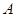 处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的
处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的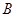 处,乙厂到河岸的垂足
处,乙厂到河岸的垂足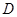 与
与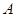 相距50千米,两厂要在此岸边
相距50千米,两厂要在此岸边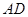 之间合建一个供水站
之间合建一个供水站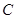 ,从供水站到甲厂和乙厂的水管费用分别为每千米3
,从供水站到甲厂和乙厂的水管费用分别为每千米3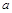 元和5
元和5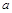 元,若
元,若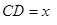 千米,设总的水管费用为
千米,设总的水管费用为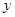 元,如图所示,
元,如图所示,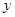 关于
关于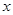 的函数表达式;
的函数表达式; 建在岸边何处才能使水管费用最省?
建在岸边何处才能使水管费用最省? 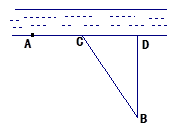
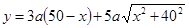 ,(2)A、D之间距甲厂20 km处
,(2)A、D之间距甲厂20 km处 点的位置即可算出到甲、乙两厂的距离,得出距离后总的水管费用即可算出。(II)水管费用最省,即求(1)式中
点的位置即可算出到甲、乙两厂的距离,得出距离后总的水管费用即可算出。(II)水管费用最省,即求(1)式中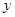 的最小值,利用求导数判断函数的单调性即可得出结果。
的最小值,利用求导数判断函数的单调性即可得出结果。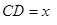 ,BD=40,AC=50-
,BD=40,AC=50-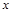 ,∴BC=
,∴BC=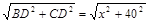
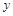 =3
=3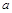 (50-x)+5
(50-x)+5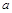
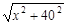
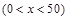 6分
6分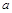 +
+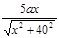 ,令y′=0,解得
,令y′=0,解得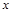 =30 8分
=30 8分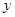 在(0,30)单调递减,在(30,50)单调递增上, 11分
在(0,30)单调递减,在(30,50)单调递增上, 11分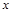 =30(km)处取得最小值,此时AC=50-
=30(km)处取得最小值,此时AC=50-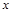 ="20(km)" 13分
="20(km)" 13分

科目:高中数学 来源:不详 题型:解答题
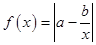 ,
, ,
,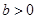 ,
,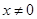 ,且满足:函数
,且满足:函数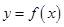 的图像与直线
的图像与直线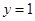 有且只有一个交点.
有且只有一个交点.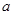 的值;
的值;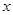 的不等式
的不等式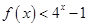 的解集为
的解集为 ,求实数
,求实数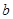 的值;
的值;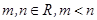 ,使得
,使得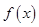 的定义域和值域均为
的定义域和值域均为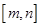 ,若存在,求出
,若存在,求出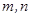 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
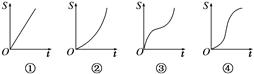
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
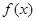 的定义域为
的定义域为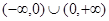 ,
,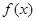 是奇函数,且当
是奇函数,且当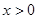 时,
时,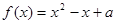 ,若函数
,若函数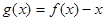 的零点恰有两个,则实数
的零点恰有两个,则实数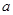 的取值范围是( )
的取值范围是( )A.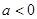 | B.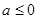 |
C.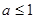 | D.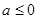 或 或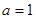 |
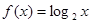 在其定义域内任意的
在其定义域内任意的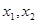 且
且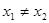 ,有如下结论:
,有如下结论: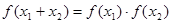 ;
;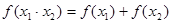 ;
;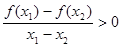 ;
;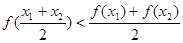 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com