
【题目】已知:以点 ![]() 为圆心的圆与x轴交于点O,A,与y轴交于点O、B,其中O为原点,
为圆心的圆与x轴交于点O,A,与y轴交于点O、B,其中O为原点,
(1)求证:△OAB的面积为定值;
(2)设直线y=﹣2x+4与圆C交于点M,N,若OM=ON,求圆C的方程.
【答案】
(1)解:∵圆C过原点O,
∴ ![]() ,
,
设圆C的方程是 ![]() ,
,
令x=0,得 ![]() ,
,
令y=0,得x1=0,x2=2t
∴ ![]() ,
,
即:△OAB的面积为定值;
(2)解:∵OM=ON,CM=CN,
∴OC垂直平分线段MN,
∵kMN=﹣2,∴ ![]() ,
,
∴直线OC的方程是 ![]() ,
,
∴ ![]() ,解得:t=2或t=﹣2,
,解得:t=2或t=﹣2,
当t=2时,圆心C的坐标为(2,1), ![]() ,
,
此时C到直线y=﹣2x+4的距离 ![]() ,
,
圆C与直线y=﹣2x+4相交于两点,
当t=﹣2时,圆心C的坐标为(﹣2,﹣1), ![]() ,
,
此时C到直线y=﹣2x+4的距离 ![]() ,
,
圆C与直线y=﹣2x+4不相交,
∴t=﹣2不符合题意舍去,
∴圆C的方程为(x﹣2)2+(y﹣1)2=5.
【解析】(1)求出半径,写出圆的方程,再解出A、B的坐标,表示出面积即可.(2)通过题意解出OC的方程,解出t 的值,直线y=﹣2x+4与圆C交于点M,N,判断t是否符合要求,可得圆的方程.
【考点精析】关于本题考查的截距式方程和圆的标准方程,需要了解直线的截距式方程:已知直线![]() 与
与![]() 轴的交点为A
轴的交点为A![]() ,与
,与![]() 轴的交点为B
轴的交点为B![]() ,其中
,其中![]() ;圆的标准方程:
;圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程才能得出正确答案.
;圆心为A(a,b),半径为r的圆的方程才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤ ![]() ),x=﹣
),x=﹣ ![]() 为f(x)的零点,x=
为f(x)的零点,x= ![]() 为y=f(x)图象的对称轴,且f(x)在(
为y=f(x)图象的对称轴,且f(x)在( ![]() ,
, ![]() )上单调,则ω的最大值为( )
)上单调,则ω的最大值为( )
A.11
B.9
C.7
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若曲线C1:x2+y2﹣2x=0与曲线C2:mx2﹣xy+mx=0有三个不同的公共点,则实数m的取值范围是( )
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
C.(﹣∞,0)∪(0,+∞)
D.(﹣ ![]() ,0)∪(0,
,0)∪(0, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2﹣12x﹣14y+60=0及其上一点A(2,4). 
(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;
(3)设点T(t,0)满足:存在圆M上的两点P和Q,使得 ![]() +
+ ![]() =
= ![]() ,求实数t的取值范围.
,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂36名工人年龄数据如图:
工人编号 | 年龄 | 工人编号 | 年龄 | 工人编号 | 年龄 | 工人编号 | 年龄 |
1 | 40 | 10 | 36 | 19 | 27 | 28 | 34 |
(1)用系统抽样法从36名工人中抽取容量为9的样本,且在第一分段里用随机抽样法抽到的年龄数据为44,列出样本的年龄数据;
(2)计算(1)中样本的均值 ![]() 和方差s2;
和方差s2;
(3)36名工人中年龄在 ![]() ﹣s和
﹣s和 ![]() +s之间有多少人?所占百分比是多少(精确到0.01%)?
+s之间有多少人?所占百分比是多少(精确到0.01%)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sin(2x+
=(sin(2x+ ![]() ),sinx),
),sinx), ![]() =(1,sinx),f(x)=
=(1,sinx),f(x)= ![]() .
.
(Ⅰ)求函数f(x)的单调递减区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,a=2 ![]() ,
, ![]() ,若
,若 ![]() sin(A+C)=2cosC,求b的大小.
sin(A+C)=2cosC,求b的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F是双曲线 ![]() =1(a>0,b>0)的左焦点,E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围为( )
=1(a>0,b>0)的左焦点,E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围为( )
A.(1,2)
B.(2,1+ ![]() )
)
C.( ![]() ,1)
,1)
D.(1+ ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图的频率分布直方图. 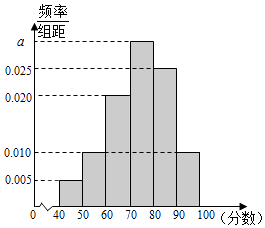
(1)求图中实数a的值;
(2)若该校高二年级共有学生640人,试估计该校高二年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com