
【题目】已知λ∈R,函数 ![]() g(x)=x2﹣4x+1+4λ,若关于x的方程f(g(x))=λ有6个解,则λ的取值范围为( )
g(x)=x2﹣4x+1+4λ,若关于x的方程f(g(x))=λ有6个解,则λ的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:
【题目】已知条件p:A={x|x2﹣2mx+m2﹣4≤0,x∈R,m∈R},条件q:B={x|x2﹣2x﹣3≤0,x∈R}.
(1)若A∩B={x|0≤x≤3},求实数m的值;
(2)若q是¬p的充分条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从椭圆![]() 上一点
上一点![]() 向
向![]() 轴作垂线,垂足恰好为椭圆的左焦点
轴作垂线,垂足恰好为椭圆的左焦点![]() ,
, ![]() 是椭圆的右顶点,
是椭圆的右顶点, ![]() 是椭圆的上顶点,且
是椭圆的上顶点,且![]() .
.
(1)求该椭圆![]() 的方程;
的方程;
(2)不过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,已知
两点,已知![]() ,直线
,直线![]() ,
, ![]() 的斜率
的斜率![]() ,
, ![]() 成等比数列,记以
成等比数列,记以![]() ,
, ![]() 为直径的圆的面积分别为
为直径的圆的面积分别为![]() ,求证;
,求证; ![]() 为定值,并求出定值.
为定值,并求出定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:(a-1)x+y+b=0,l2:ax+by-4=0,求满足下列条件的a,b的值.
(1)l1⊥l2,且l1过点(1,1);
(2)l1∥l2,且l2在第一象限内与两坐标轴围成的三角形的面积为2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,
, ![]() 为椭圆
为椭圆![]() 上的任意一点(不含长轴端点),且
上的任意一点(不含长轴端点),且![]() 面积的最大值为1.
面积的最大值为1.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且线段
,且线段![]() 的中点不在圆
的中点不在圆![]() 内,求
内,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了![]() 人,回答问题计结果如下图表所示:
人,回答问题计结果如下图表所示:

(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
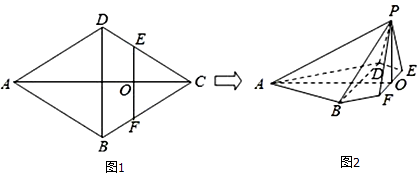
【题目】如图1所示,在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,EF∩AC=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图2所示五棱锥P﹣ABFED,且AP= ![]() ,
, 
(1)求证:BD⊥平面POA;
(2)求二面角B﹣AP﹣O的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com