
【题目】已知曲线C的参数方程为 ![]() (α为参数),以直角坐标系原点为极点,Ox轴正半轴为极轴建立极坐标系.
(α为参数),以直角坐标系原点为极点,Ox轴正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程
(2)若直线l的极坐标方程为ρ(sinθ+cosθ)=1,求直线l被曲线C截得的弦长.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2﹣a)lnx+ ![]() +2ax(a∈R).
+2ax(a∈R).
(Ⅰ)当a=0时,求f(x)的极值;
(Ⅱ)当a<0时,求f(x)单调区间;
(Ⅲ)若对任意a∈(﹣3,﹣2)及x1 , x2∈[1,3],恒有(m+ln3)a﹣2ln3>|f(x1)﹣f(x2)|成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4﹣4:坐标系与参数方程)
已知直线l过点P(﹣1,2),且倾斜角为 ![]() ,圆方程为
,圆方程为 ![]() .
.
(1)求直线l的参数方程;
(2)设直线l与圆交与M、N两点,求|PM||PN|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A′B′C′中,AA′=2AC=2BC,E为AA′的中点,C′E⊥BE. 
(1)求证:C′E⊥平面BCE;
(2)求直线AB′与平面BEC′所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图所示.

(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.

求证:(1)DE∥平面AA1C1C;
(2)BC1⊥AB1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,侧面PAD是边长为2的等边三角形且垂直于底![]() ,
, ![]()
![]() 是
是![]() 的中点。
的中点。
(1)证明:直线![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上,且直线
上,且直线![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国乒乓球队备战里约奥运会热身赛暨选拨赛于2016年7月14日在山东威海开赛,种子选手A与非种子选手B1 , B2 , B3分别进行一场对抗赛,按以往多次比赛的统计,A获胜的概率分别为 ![]() ,且各场比赛互不影响.
,且各场比赛互不影响.
(Ⅰ)若A至少获胜两场的概率大于 ![]() ,则A入选征战里约奥运会的最终名单,否则不予入选,问A是否会入选最终的名单?
,则A入选征战里约奥运会的最终名单,否则不予入选,问A是否会入选最终的名单?
(Ⅱ)求A获胜场数X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知产品![]() 的质量采用综合指标值
的质量采用综合指标值![]() 进行衡量,
进行衡量,![]() 为一等品;
为一等品;![]() 为二等品;
为二等品;![]() 为三等品.我市一家工厂准备购进新型设备以提高生产产品
为三等品.我市一家工厂准备购进新型设备以提高生产产品![]() 的效益,在某供应商提供的设备中任选一个试用,生产了一批产品并统计相关数据,得到频率分布直方图:
的效益,在某供应商提供的设备中任选一个试用,生产了一批产品并统计相关数据,得到频率分布直方图:
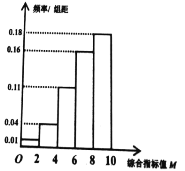
(1)估计该新型设备生产的产品![]() 为二等品的概率;
为二等品的概率;
(2)根据这家工厂的记录,产品各等次的销售率(某等次产品销量与其对应产量的比值)及单件售价情况如下:
一等品 | 二等品 | 三等品 | |
销售率 |
|
|
|
单件售价 |
|
|
|
根据以往的销售方案,未售出的产品统一按原售价的![]() 全部处理完.已知该工厂认购该新型设备的前提条件是,该新型设备生产的产品同时满足下列两个条件:
全部处理完.已知该工厂认购该新型设备的前提条件是,该新型设备生产的产品同时满足下列两个条件:
①综合指标值的平均数不小于![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
②单件平均利润值不低于![]() .
.
若该新型设备生产的产品![]() 的成本为
的成本为![]() 元/件,月产量为
元/件,月产量为![]() 件,在销售方案不变的情况下,根据以上图表数据,分析该新型设备是否达到该工厂的认购条件.
件,在销售方案不变的情况下,根据以上图表数据,分析该新型设备是否达到该工厂的认购条件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com