
【题目】如图所示,在三棱锥A-BOC中,OA⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=![]() ,动点D在线段AB上.
,动点D在线段AB上.

(1)求证:平面COD⊥平面AOB;
(2)当OD⊥AB时,求三棱锥C-OBD的体积.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)欲证平面COD⊥平面AOB,根据面面垂直的判定定理可知在平面COD内一直线与平面AOB垂直,根据勾股定理可知OC⊥OB,根据线面垂直的判定定理可知OC⊥平面AOB,而OC平面COD,满足定理所需条件;(2)OD⊥AB,OD=![]() ,此时,BD=1.根据三棱锥的体积公式求出所求即可
,此时,BD=1.根据三棱锥的体积公式求出所求即可
试题解析:(1)∵AO⊥底面BOC,
∴AO⊥OC,
AO⊥OB. ……3
∵∠OAB=∠OAC=30°,AB=AC=4,
∴OC=OB=2.
又BC=2![]() ,
,
∴OC⊥OB, ……6
∴OC⊥平面AOB.
∵OC![]() 平面COD,
平面COD,
∴平面COD⊥平面AOB. ……9
(2)∵OD⊥AB,∴BD=1,OD=![]() .
.
∴VC-OBD =![]() ×
×![]() ×
×![]() ×1×2=
×1×2=![]() ……12
……12


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】高中流行这样一句话“文科就怕数学不好,理科就怕英语不好”.下表是一次针对高三文科学生的调查所得的数据,试问:在出错概率不超过0.01的前提下文科学生总成绩不好与数学成绩不好有关系吗?
总成绩好 | 总成绩不好 | 总计 | |
数学成绩好 | 20 | 10 | 30 |
数学成绩不好 | 5 | 15 | 20 |
总计 | 25 | 25 | 50 |
(P(K2≥3.841)≈0.05,P(K2≥6.635)≈0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(Ⅰ)设f(x)= 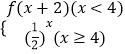 ,求f(1+log23)的值;
,求f(1+log23)的值;
(Ⅱ)已知g(x)=ln[(m2﹣1)x2﹣(1﹣m)x+1]的定义域为R,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2(a+2)x+a2 , g(x)=﹣x2+2(a﹣2)x﹣a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)},(其中max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A﹣B=( )
A.a2﹣2a﹣16
B.a2+2a﹣16
C.﹣16
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O、A、B三地在同一水平面内,A地在O地正东方向2km处,B地在O地正北方向2km处,某测绘队员在A、B之间的直线公路上任选一点C作为测绘点,用测绘仪进行测绘,O地为一磁场,距离其不超过![]() km的范围内会测绘仪等电子仪器形成干扰,使测量结果不准确,则该测绘队员能够得到准确数据的概率是( )
km的范围内会测绘仪等电子仪器形成干扰,使测量结果不准确,则该测绘队员能够得到准确数据的概率是( )
A.1-![]()
B.![]()
C.1-![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 若f(x1)=f(x2),且x1<x2,关于下列命题:(1)f(x1)>f(﹣x2);(2)f(x2)>f(﹣x1);(3)f(x1)>f(﹣x1);(4)f(x2)>f(﹣x2).正确的个数为( )
若f(x1)=f(x2),且x1<x2,关于下列命题:(1)f(x1)>f(﹣x2);(2)f(x2)>f(﹣x1);(3)f(x1)>f(﹣x1);(4)f(x2)>f(﹣x2).正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com