
【题目】某工厂用7万元钱购买了一台新机器,运输安装费用2千元,每年投保、动力消耗的费用也为2千元,每年的保养、维修、更换易损零件的费用逐年增加,第一年为2千元,第二年为3千元,第三年为4千元,依此类推,即每年增加1千元.
(1)求使用n年后,保养、维修、更换易损零件的累计费用S(千元)关于n的表达式;
(2)问这台机器最佳使用年限是多少年?并求出年平均费用(单位:千元)的最小值.(最佳使用年限是指使年平均费用最小的时间,年平均费用=(购入机器费用+运输安装费用+每年投保、动力消耗的费用+保养、维修、更换易损零件的累计费用)÷机器使用的年数)
科目:高中数学 来源: 题型:
【题目】如图,公园里有一湖泊,其边界由两条线段![]() 和以
和以![]() 为直径的半圆弧
为直径的半圆弧![]() 组成,其中
组成,其中![]() 为2百米,
为2百米,![]() 为
为![]() .若在半圆弧
.若在半圆弧![]() ,线段
,线段![]() ,线段
,线段![]() 上各建一个观赏亭
上各建一个观赏亭![]() ,再修两条栈道
,再修两条栈道![]() ,使
,使![]() . 记
. 记![]() .
.

(1)试用![]() 表示
表示![]() 的长;
的长;
(2)试确定点![]() 的位置,使两条栈道长度之和最大.
的位置,使两条栈道长度之和最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在直角坐标系xOy中,设倾斜角为α的直线l:![]() (t为参数)与曲线C:
(t为参数)与曲线C:![]() (θ为参数)相交于不同的两点A,B.
(θ为参数)相交于不同的两点A,B.
(Ⅰ)若α=![]() ,求线段AB中点M的坐标;
,求线段AB中点M的坐标;
(Ⅱ)若|PA|·|PB|=|OP|![]() ,其中P(2,
,其中P(2,![]() ),求直线l的斜率.
),求直线l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
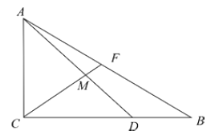
【题目】在三角形ABC中,![]() ,
,![]() ,
,![]() ,D是线段BC上一点,且
,D是线段BC上一点,且![]() ,F为线段AB上一点.
,F为线段AB上一点.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)求![]() 的取值范围;
的取值范围;
(3)若![]() 为线段
为线段![]() 的中点,直线
的中点,直线![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}满足a1=1,且an+1-an=n+1(n∈N*),则数列{an}的通项公式为________; ![]() 前10项的和为________.
前10项的和为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项的和记为Sn.如果a4=-12,a8=-4.
(1)求数列{an}的通项公式;
(2)求Sn的最小值及其相应的n的值;
(3)从数列{an}中依次取出a1,a2,a4,a8,…,![]() ,…,构成一个新的数列{bn},求{bn}的前n项和
,…,构成一个新的数列{bn},求{bn}的前n项和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)经过点(1,
=1(a>b>0)经过点(1,![]() ),且焦距为2
),且焦距为2![]() .
.
(1)求椭圆C方程;
(2)椭圆C的左,右焦点分别为F1,F2,过点F2的直线l与椭圆C交于A,B两点,求△F2AB面积S的最大值并求出相应直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
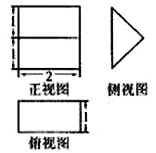
【题目】《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的外接球的表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
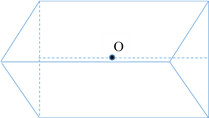
【解析】几何体如图,球心为O,半径为![]() ,表面积为
,表面积为![]() ,选B.
,选B.
点睛:涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.
【题型】单选题
【结束】
9
【题目】![]() 是双曲线
是双曲线![]() 的左右焦点,过
的左右焦点,过![]() 且斜率为1的直线与两条渐近线分别交于
且斜率为1的直线与两条渐近线分别交于![]() 两点,若
两点,若![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com