
【题目】已知点![]() ,
,![]() ,点
,点![]() 为曲线
为曲线![]() 上任意一点且满足
上任意一点且满足![]()
(1)求曲线![]() 的方程;
的方程;
(2)设曲线![]() 与
与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 是曲线
是曲线![]() 上异于
上异于![]() 的任意一点,直线
的任意一点,直线![]() 分别交直线
分别交直线![]() :
:![]() 于点
于点![]() ,试问
,试问![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在点
;(2)存在点![]() 使得
使得![]() 成立.
成立. ![]()
【解析】
(1)设P(x,y),由|PA|=2|PB|,得![]() =2
=2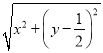 ,由此能求出曲线
,由此能求出曲线![]() 的方程.
的方程.
(2)由题意得M(0,1),N(0,-1),设点R(x0,y0),(x0≠0),由点R在曲线![]() 上,得
上,得![]() =1,直线RM的方程
=1,直线RM的方程![]() ,从而直线RM与直线y=3的交点为
,从而直线RM与直线y=3的交点为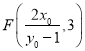 ,直线RN的方程为
,直线RN的方程为![]() ,从而直线RN与直线y=3的交点为
,从而直线RN与直线y=3的交点为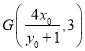 ,假设存在点S(0,m),使得
,假设存在点S(0,m),使得![]() 成立,则
成立,则![]() ,由此能求出存在点S,使得
,由此能求出存在点S,使得![]() 成立,且S点的坐标为
成立,且S点的坐标为![]() .
.
(1)设![]() ,由
,由![]() ,
,
得: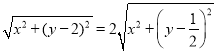 ,
,
整理得![]() .
.
所以曲线![]() 的方程为
的方程为![]() .
.
(2)由题意得,![]() ,
,![]() .
.
设点![]() ,由点
,由点![]() 在曲线
在曲线![]() 上,
上,
所以![]() .
.
直线![]() 的方程为
的方程为![]() ,
,
所以直线![]() 与直线
与直线![]() 的交点为
的交点为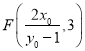 .
.
直线![]() 的方程为
的方程为![]()
所以直线![]() 与直线
与直线![]() 的交点为
的交点为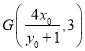 .
.
假设存在点![]() ,使得
,使得![]() 成立,
成立,
则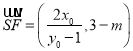 ,
,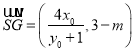 .
.
即![]() ,
,
整理得![]() .
.
因为![]() ,
,
所以![]() ,
,
解得![]() .
.
所以存在点![]() 使得
使得![]() 成立,且点
成立,且点![]() 的坐标为
的坐标为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在某互联网大会上,为了提升安全级别,将5名特警分配到3个重要路口执勤,每个人只能选择一个路口,每个路口最少1人,最多3人,且甲和乙不能安排在同一个路口,则不同的安排方法有( )
A. 180种 B. 150种 C. 96种 D. 114种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() ,则下列说法不正确的是( )
,则下列说法不正确的是( )
A.其图象开口向上,且始终与![]() 轴有两个不同的交点
轴有两个不同的交点
B.无论![]() 取何实数,其图象始终过定点
取何实数,其图象始终过定点![]()
C.其图象对称轴的位置没有确定,但其形状不会因![]() 的取值不同而改变
的取值不同而改变
D.函数的最小值大于![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族![]() 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当![]() 中
中![]() (
(![]() )的成员自驾时,自驾群体的人均通勤时间为
)的成员自驾时,自驾群体的人均通勤时间为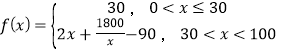 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受![]() 影响,恒为
影响,恒为![]() 分钟,试根据上述分析结果回答下列问题:
分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族![]() 的人均通勤时间
的人均通勤时间![]() 的表达式;讨论
的表达式;讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将5名报名参加运动会的同学分别安排到跳绳、接力,投篮三项比赛中(假设这些比赛都不设人数上限),每人只参加一项,则共有![]() 种不同的方案;若每项比赛至少要安排一人时,则共有
种不同的方案;若每项比赛至少要安排一人时,则共有![]() 种不同的方案,其中
种不同的方案,其中![]() 的值为( )
的值为( )
A. 543 B. 425 C. 393 D. 275
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(ax2+2x+3).
(1)若f(1)=1,求f(x)的单调区间;
(2)是否存在实数a,使f(x)的最小值为0?若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com