
【题目】已知在直角坐标系![]() 中,曲线
中,曲线![]() 的方程是
的方程是![]() ,直线
,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)写出曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知cos(α﹣β)=﹣ ![]() ,cos(α+β)=
,cos(α+β)= ![]() ,且(α﹣β)∈(
,且(α﹣β)∈( ![]() ,π),(α+β)∈(
,π),(α+β)∈( ![]() ,2π),则cos2α=( )
,2π),则cos2α=( )
A.﹣1
B.﹣ ![]()
C.![]()
D.﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为 (
(![]() 为参数,
为参数, ![]() ),以
),以![]() 为极点,
为极点, ![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆 ![]() +
+ ![]() =1(a>b>0)的左右焦点分别为F1 , F2 , 点D在椭圆上,DF1⊥F1F2 ,
=1(a>b>0)的左右焦点分别为F1 , F2 , 点D在椭圆上,DF1⊥F1F2 , ![]() =2
=2 ![]() ,△DF1F2的面积为
,△DF1F2的面积为 ![]() . (Ⅰ)求该椭圆的标准方程;
. (Ⅰ)求该椭圆的标准方程;
(Ⅱ)是否存在圆心在y轴上的圆,使圆在x轴的上方与椭圆有两个交点,且圆在这两个交点处的两条切线互相垂直并分别过不同的焦点?若存在,求出圆的方程;若不存在,请说明理由.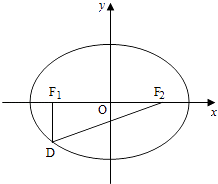
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 表示大于
表示大于![]() 的整数
的整数![]() 的十位数,例如
的十位数,例如![]() ,
,![]() .已知
.已知![]() ,
,![]() ,
,![]() 都是大于
都是大于![]() 的互不相等的整数,现有如下
的互不相等的整数,现有如下![]() 个命题:
个命题:
①若![]() ,则
,则![]() ;②
;②![]() ,
,![]() 且
且![]() ;
;
③若![]() 是质数,则
是质数,则![]() 也是质数;④若
也是质数;④若![]() ,
,![]() ,
,![]() 成等差数列,则
成等差数列,则![]() ,
,![]() ,
,![]() 可能成等比数列.
可能成等比数列.
其中所有的真命题为( )
A. ② B. ③④ C. ①②④ D. ①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为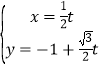 (
(![]() 为参数),且直线
为参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,以直角坐标系的原点为极点,以
两点,以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2) 已知点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|. (Ⅰ)解不等式f(x+8)≥10﹣f(x);
(Ⅱ)若|x|>1,|y|<1,求证:f(y)<|x|f( ![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com