
【题目】已知![]() ,
,![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,若关于
时,若关于![]() 的方程
的方程![]() 存在两个正实数根
存在两个正实数根![]() ,证明:
,证明:![]() 且
且![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)求出函数的导函数,再计算出![]() ,
,![]() ,即可求出切线方程;
,即可求出切线方程;
(2)由![]() 存在两个正实数根
存在两个正实数根![]() ,整理得方程
,整理得方程![]() 存在两个正实数根
存在两个正实数根![]() .令
.令![]() 利用导数研究其单调性、最值,因为
利用导数研究其单调性、最值,因为![]() 有两个零点,即
有两个零点,即![]() ,得
,得![]() .
.
因为实数![]() ,
,![]() 是
是![]() 的两个根,所以
的两个根,所以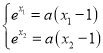 ,从而
,从而![]() .令
.令![]() ,
,![]() ,则
,则![]() ,变形整理得
,变形整理得![]() .要证
.要证![]() ,则只需证
,则只需证![]() ,即只要证
,即只要证![]() ,
,
再构造函数即可证明.
(1)解:∵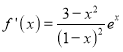 ,
,
∴![]() ,
,![]() ,
,
∴曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(2)证明:由![]() 存在两个正实数根
存在两个正实数根![]() ,
,
整理得方程![]() 存在两个正实数根
存在两个正实数根![]() .
.
由![]() ,知
,知![]() ,
,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减.
上单调递减.
所以![]() .
.
因为![]() 有两个零点,即
有两个零点,即![]() ,得
,得![]() .
.
因为实数![]() ,
,![]() 是
是![]() 的两个根,
的两个根,
所以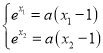 ,从而
,从而![]() .
.
令![]() ,
,![]() ,则
,则![]() ,变形整理得
,变形整理得![]() .
.
要证![]() ,则只需证
,则只需证![]() ,即只要证
,即只要证![]() ,
,
结合对数函数![]() 的图象可知,只需要证
的图象可知,只需要证![]() ,
,![]() 两点连线的斜率要比
两点连线的斜率要比![]() ,
,![]() 两点连线的斜率小即可.
两点连线的斜率小即可.
因为![]() ,所以只要证
,所以只要证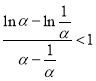 ,整理得
,整理得![]() .
.
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递减,即
上单调递减,即![]() ,
,
所以![]() 成立,故
成立,故![]() 成立.
成立.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】汽车尾气中含有一氧化碳(![]() ),碳氢化合物(
),碳氢化合物(![]() )等污染物,是环境污染的主要因素之一,汽车在使用若干年之后排放的尾气中的污染物会出现递增的现象,所以国家根据机动车使用和安全技术、排放检验状况,对达到报废标准的机动车实施强制报废.某环保组织为了解公众对机动车强制报废标准的了解情况,随机调查了100人,所得数据制成如下列联表:
)等污染物,是环境污染的主要因素之一,汽车在使用若干年之后排放的尾气中的污染物会出现递增的现象,所以国家根据机动车使用和安全技术、排放检验状况,对达到报废标准的机动车实施强制报废.某环保组织为了解公众对机动车强制报废标准的了解情况,随机调查了100人,所得数据制成如下列联表:
不了解 | 了解 | 总计 | |
女性 |
|
| 50 |
男性 | 15 | 35 | 50 |
总计 |
|
| 100 |
(1)若从这100人中任选1人,选到了解机动车强制报废标准的人的概率为![]() ,问是否有
,问是否有![]() 的把握认为“对机动车强制报废标准是否了解与性别有关”?
的把握认为“对机动车强制报废标准是否了解与性别有关”?
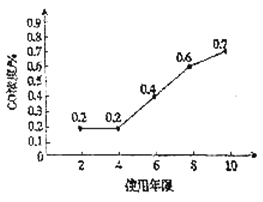
(2)该环保组织从相关部门获得某型号汽车的使用年限与排放的尾气中![]() 浓度的数据,并制成如图所示的折线图,若该型号汽车的使用年限不超过15年,可近似认为排放的尾气中
浓度的数据,并制成如图所示的折线图,若该型号汽车的使用年限不超过15年,可近似认为排放的尾气中![]() 浓度
浓度![]() 与使用年限
与使用年限![]() 线性相关,试确定
线性相关,试确定![]() 关于
关于![]() 的回归方程,并预测该型号的汽车使用12年排放尾气中的
的回归方程,并预测该型号的汽车使用12年排放尾气中的![]() 浓度是使用4年的多少倍.
浓度是使用4年的多少倍.
附: (
(![]() )
)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:用最小二乘法求线性回归方程系数公式: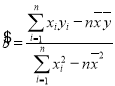 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了了解该企业工人组装某产品所用时间,对每个工人组装一个该产品的用时作了记录,得到大量统计数据.从这些统计数据中随机抽取了![]() 个数据作为样本,得到如图所示的茎叶图(单位:分钟).若用时不超过
个数据作为样本,得到如图所示的茎叶图(单位:分钟).若用时不超过![]() (分钟),则称这个工人为优秀员工.
(分钟),则称这个工人为优秀员工.
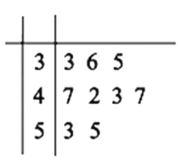
(1)求这个样本数据的中位数和众数;
(2)以这![]() 个样本数据中优秀员工的频率作为概率,任意调查
个样本数据中优秀员工的频率作为概率,任意调查![]() 名工人,求被调查的
名工人,求被调查的![]() 名工人中优秀员工的数量
名工人中优秀员工的数量![]() 分布列和数学期望.
分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝时期的数学家祖暅提出了计算体积的祖暅原理:“幂势既同,则积不容异。”意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.已知曲线![]() ,直线
,直线![]() 为曲线
为曲线![]() 在点
在点![]() 处的切线.如图所示,阴影部分为曲线
处的切线.如图所示,阴影部分为曲线![]() 、直线
、直线![]() 以及
以及![]() 轴所围成的平面图形,记该平面图形绕
轴所围成的平面图形,记该平面图形绕![]() 轴旋转一周所得的几何体为
轴旋转一周所得的几何体为![]() .给出以下四个几何体:
.给出以下四个几何体:
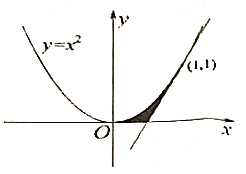
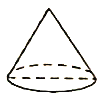
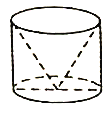


① ② ③ ④
图①是底面直径和高均为![]() 的圆锥;
的圆锥;
图②是将底面直径和高均为![]() 的圆柱挖掉一个与圆柱同底等高的倒置圆锥得到的几何体;
的圆柱挖掉一个与圆柱同底等高的倒置圆锥得到的几何体;
图③是底面边长和高均为![]() 的正四棱锥;
的正四棱锥;
图④是将上底面直径为![]() ,下底面直径为
,下底面直径为![]() ,高为
,高为![]() 的圆台挖掉一个底面直径为
的圆台挖掉一个底面直径为![]() ,高为
,高为![]() 的倒置圆锥得到的几何体.
的倒置圆锥得到的几何体.
根据祖暅原理,以上四个几何体中与![]() 的体积相等的是( )
的体积相等的是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在古装电视剧《知否》中,甲乙两人进行一种投壶比赛,比赛投中得分情况分“有初”“贯耳”“散射”“双耳”“依竿”五种,其中“有初”算“两筹”,“贯耳”算“四筹”,“散射”算“五筹”,“双耳”算“六筹”,“依竿”算“十筹”,三场比赛得筹数最多者获胜.假设甲投中“有初”的概率为![]() ,投中“贯耳”的概率为
,投中“贯耳”的概率为![]() ,投中“散射”的概率为
,投中“散射”的概率为![]() ,投中“双耳”的概率为
,投中“双耳”的概率为![]() ,投中“依竿”的概率为
,投中“依竿”的概率为![]() ,乙的投掷水平与甲相同,且甲乙投掷相互独立.比赛第一场,两人平局;第二场,甲投了个“贯耳”,乙投了个“双耳”,则三场比赛结束时,甲获胜的概率为( )
,乙的投掷水平与甲相同,且甲乙投掷相互独立.比赛第一场,两人平局;第二场,甲投了个“贯耳”,乙投了个“双耳”,则三场比赛结束时,甲获胜的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,底面ABCD是边长为2的菱形,![]() ,
,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,BE与平面ABCD所成的角为
,BE与平面ABCD所成的角为![]() .
.
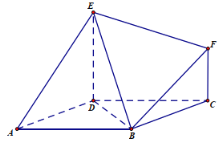
(1)求证:平面![]() 平面BDE;
平面BDE;
(2)求二面角B-EF-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图象关于直线
,其图象关于直线![]() 对称,为了得到函数
对称,为了得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象上的所有点( )
的图象上的所有点( )
A.先向左平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
B.先向右平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
C.先向右平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
D.先向左平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 的各条棱长均相等,
的各条棱长均相等, ![]() 为
为![]() 的中点,
的中点, ![]() 分别是线段
分别是线段![]() 和线段
和线段![]() 上的动点(含端点),且满足
上的动点(含端点),且满足![]() .当
.当![]() 运动时,下列结论中不正确的是( )
运动时,下列结论中不正确的是( )
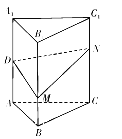
A. 平面![]() 平面
平面![]() B. 三棱锥
B. 三棱锥![]() 的体积为定值
的体积为定值
C. ![]() 可能为直角三角形 D. 平面
可能为直角三角形 D. 平面![]() 与平面
与平面![]() 所成的锐二面角范围为
所成的锐二面角范围为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com