
 和
和 ,点T(x,y)满足
,点T(x,y)满足 ,O为直角坐标原点,
,O为直角坐标原点,
 ,故轨迹是以F1,F2为焦点的椭圆,从而可求轨迹方程;
,故轨迹是以F1,F2为焦点的椭圆,从而可求轨迹方程;
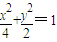 (6分)
(6分) 消去y得:(1+2k2)x2+4ktx+2t2-4=0,(9分)
消去y得:(1+2k2)x2+4ktx+2t2-4=0,(9分) (10分)
(10分) (12分)
(12分)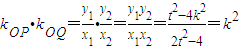 ,(14分)∴
,(14分)∴ ∴
∴ (16分)
(16分)

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
 (理)已知椭圆
(理)已知椭圆| x2 | a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2 |
| TF1 |
| TF2 |
查看答案和解析>>
科目:高中数学 来源:吉林省吉林一中2011-2012学年高三阶段验收试题数学 题型:解答题
(理)已知数列{an}的前n项和 ,且
,且 =1,
=1,
 .
.
(I)求数列{an}的通项公式;
(II)已知定理:“若函数f(x)在区间D上是凹函数,x>y(x,y∈D),且f’(x)存在,则有
< f’(x)”.若且函数y=xn+1 在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
(III)求证:≤bn<2.
 (文)如图,|AB|=2,O为AB中点,直线
(文)如图,|AB|=2,O为AB中点,直线 过B且垂直于AB,过A的动直线与
过B且垂直于AB,过A的动直线与 交于点C,点M在线段AC上,满足=.
交于点C,点M在线段AC上,满足=.
(I)求点M的轨迹方程;
(II)若过B点且斜率为- 的直线与轨迹M交于
点P,点Q(t,0)是x轴上任意一点,求当ΔBPQ为
锐角三角形时t的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011年上海市奉贤区高考数学三模试卷(文理合卷)(解析版) 题型:解答题
 和
和 ,点T(x,y)满足
,点T(x,y)满足 ,O为直角坐标原点,
,O为直角坐标原点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com