设a∈[0,2],b∈[0,4],则函数f(x)=x2+2ax+b在R上有两个不同零点的概率为 ________.

分析:欲求函数f(x)=x
2+2ax+b在R上有两个不同零点的概率,则可建立关于a,b的直角坐标系,画出关于a和b的平面区域,再根据几何概型概率公式结合定积分求面积的方法易求解.
解答:
解:∵函数f(x)=x
2+2ax+b在R上有两个不同零点,
∴△≥0,即b≤a
2.
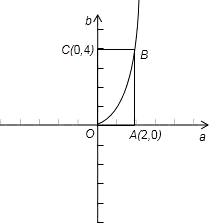
则建立关于a,b的直角坐标系,画出关于a和b的平面区域,如图.
此时,可知此题求解的概率类型为关于面积的几何概型,
由图可知基本事件空间所对应的几何度量S(Ω)=8,满足b≤a
2.
由于
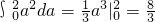
.所以P=
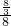
=

.
故答案为:

.
点评:本题综合考查了二次函数的图象与性质,函数的零点,几何概型,及定积分在求面积中的应用,是一道综合性比较强的题目,考生容易在建立直角坐标系中出错,可多参考本题的做法.


 解:∵函数f(x)=x2+2ax+b在R上有两个不同零点,
解:∵函数f(x)=x2+2ax+b在R上有两个不同零点,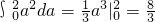 .所以P=
.所以P=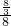 =
= .
. .
.
