
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴不重合,
轴不重合, ![]() 交圆
交圆![]() 于
于![]() 两点,过
两点,过![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)证明![]() 为定值,并写出点
为定值,并写出点![]() 的轨迹方程;
的轨迹方程;
(2)设![]() ,过点
,过点![]() 作直线
作直线![]() ,交点
,交点![]() 的轨迹于
的轨迹于![]() 两点 (异于
两点 (异于![]() ),直线
),直线![]() 的斜率分别为
的斜率分别为![]() ,证明:
,证明: ![]() 为定值.
为定值.
科目:高中数学 来源: 题型:
【题目】中国铁路总公司相关负责人表示,到2018年底,全国铁路营业里程达到13.1万公里,其中高铁营业里程2.9万公里,超过世界高铁总里程的三分之二,下图是2014年到2018年铁路和高铁运营里程(单位:万公里)的折线图,以下结论不正确的是( )

A.每相邻两年相比较,2014年到2015年铁路运营里程增加最显著
B.从2014年到2018年这5年,高铁运营里程与年价正相关
C.2018年高铁运营里程比2014年高铁运营里程增长80%以上
D.从2014年到2018年这5年,高铁运营里程数依次成等差数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,
,![]() 为椭圆
为椭圆![]() 上两点,圆
上两点,圆![]() .
.
(1)若![]() 轴,且满足直线
轴,且满足直线![]() 与圆
与圆![]() 相切,求圆
相切,求圆![]() 的方程;
的方程;
(2)若圆![]() 的半径为
的半径为![]() ,点
,点![]() 满足
满足![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值.
截得弦长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
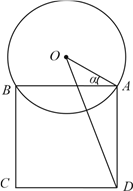
【题目】某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设![]() .(注:底面直径和高相等的圆柱叫做等边圆柱.)
.(注:底面直径和高相等的圆柱叫做等边圆柱.)
(1)用![]() 表示圆柱的高;
表示圆柱的高;
(2)实践表明,当球心![]() 和圆柱底面圆周上的点
和圆柱底面圆周上的点![]() 的距离达到最大时,景观的观赏效
的距离达到最大时,景观的观赏效
果最佳,求此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三家企业产品的成本分别为10000,12000,15000,其成本构成如下图所示,则关于这三家企业下列说法错误的是( )
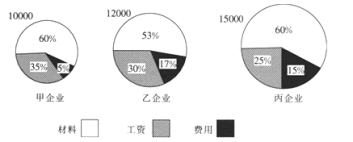
A.成本最大的企业是丙企业B.费用支出最高的企业是丙企业
C.支付工资最少的企业是乙企业D.材料成本最高的企业是丙企业
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面ABCD⊥平面CDEF,且四边形ABCD是梯形,四边形CDEF是矩形,![]()
![]() ,M是线段DE上的点,满足DM=2ME.
,M是线段DE上的点,满足DM=2ME.
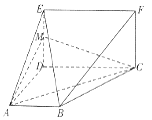
(1)证明:BE//平面MAC;
(2)求直线BF与平面MAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() 为偶函数,求
为偶函数,求![]() 的值并写出
的值并写出![]() 的增区间;
的增区间;
(Ⅱ)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,当
,当![]() 时,求
时,求![]() 的最小值;
的最小值;
(Ⅲ)对任意的![]() ,
,![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com