
【题目】设![]() .
.
(1)讨论![]() 在
在![]() 上的单调性;
上的单调性;
(2)令![]() ,试证明
,试证明![]() 在
在![]() 上有且仅有三个零点.
上有且仅有三个零点.
【答案】(1)![]() 的单调递增区间是
的单调递增区间是![]() ,递减区间是
,递减区间是![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)首先求导得到![]() ,再根据导函数的正负性即可得到函数的单调区间.
,再根据导函数的正负性即可得到函数的单调区间.
(2)首先根据![]() ,
,![]() 得到
得到![]() 是
是![]() 的一个零点,再根据
的一个零点,再根据![]() 是偶函数得到
是偶函数得到![]() 在
在![]() 上的零点个数,只需确定
上的零点个数,只需确定![]() 时,
时,![]() 的零点个数即可,再求出
的零点个数即可,再求出![]() 在
在![]() 时的单调性和最值,确定其零点个数即可.
时的单调性和最值,确定其零点个数即可.
![]() ,
,
令![]() ,则
,则![]() 或
或![]() .
.
![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
![]() 时
时![]() ,
,![]() 单调递减,
单调递减,
![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
![]() 的单调递增区间是
的单调递增区间是![]() ,
,
递减区间是![]() .
.
(2)![]() ,
,
因为![]() ,所以
,所以![]() 是
是![]() 的一个零点.
的一个零点.
![]()
所以![]() 是偶函数,
是偶函数,
即要确定![]() 在
在![]() 上的零点个数,需确定
上的零点个数,需确定![]() 时,
时,![]() 的零点个数即可.
的零点个数即可.
①当![]() 时,
时,![]()
令![]() ,即
,即![]() 或
或![]()
![]() .
.
![]() 时,
时,![]() 单调递减,
单调递减,
且![]() ,
,
![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
且![]()
![]() 在
在![]() 有唯一零点
有唯一零点
②当![]() 时,由于
时,由于![]() ,
,![]() .
.
![]()
![]()
而![]() 在
在![]() 单调递增,
单调递增,![]()
所以![]() 恒成立,故
恒成立,故![]() 在
在![]() 无零点,
无零点,
所以![]() 在
在![]() 有一个零点,
有一个零点,
由于![]() 是偶函数,所以
是偶函数,所以![]() 在
在![]() 有一个零点,而
有一个零点,而![]() ,
,
综上![]() 在
在![]() 有且仅有三个零点.
有且仅有三个零点.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右顶点为A,上顶点为B,O为坐标原原点,点O到直线AB的距离为
的右顶点为A,上顶点为B,O为坐标原原点,点O到直线AB的距离为![]() ,
,![]() 的面积为1.
的面积为1.
(1)求榷圆的标准方程;
(2)直线![]() 与椭圆交于C,D两点,若直线
与椭圆交于C,D两点,若直线![]() 直线AB,设直线AC,BD的斜率分别为
直线AB,设直线AC,BD的斜率分别为![]() 证明:
证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放40年来,我国城市基础设施发生了巨大的变化,各种交通工具大大方便了人们的出行需求.某城市的A先生实行的是早九晚五的工作时间,上班通常乘坐公交或地铁加步行.已知从家到最近的公交站或地铁站都需步行5分钟,乘坐公交到离单位最近的公交站所需时间Z1(单位:分钟)服从正态分布N(33,42),下车后步行再到单位需要12分钟;乘坐地铁到离单位最近的地铁站所需时间Z2(单位:分钟)服从正态分布N(44,22),从地铁站步行到单位需要5分钟.现有下列说法:①若8:00出门,则乘坐公交一定不会迟到;②若8:02出门,则乘坐公交和地铁上班迟到的可能性相同;③若8:06出门,则乘坐公交比地铁上班迟到的可能性大;④若8:12出门,则乘坐地铁比公交上班迟到的可能性大.则以上说法中正确的序号是_____.
参考数据:若Z~N(μ,σ2),则P(μ﹣σ<Z≤μ+σ)=0.6826,P(μ﹣2σ<Z≤μ+2σ)=0.9544,P(μ﹣3σ<Z≤μ+3σ)=0.9974
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全民参与是打赢新型冠状病毒防疫战的根本方法.在防控疫情的过程中,某小区的“卡口”工作人员由“社区工作者”“下沉干部”“志愿者”三种身份的人员构成,其中社区工作者3人,下沉干部2人,志愿者1人.某电视台某天上午随机抽取2人进行访谈,某报社在该天下午随机抽取1人进行访谈.
(1)设![]() 表示上午抽到的社区工作者的人数,求随机变量
表示上午抽到的社区工作者的人数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)设![]() 为事件“全天抽到的
为事件“全天抽到的![]() 名工作人员的身份互不相同”,求事件
名工作人员的身份互不相同”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了比较两种治疗某病毒的药(分别称为甲药,乙药)的疗效,某医疗团队随机地选取了服用甲药的患者和服用乙药的患者进行研究,根据研究的数据,绘制了如图1等高条形图
.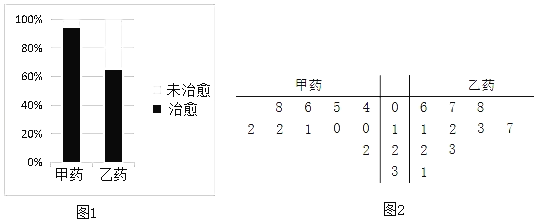
(1)根据等高条形图,判断哪一种药的治愈率更高,不用说明理由;
(2)为了进一步研究两种药的疗效,从服用甲药的治愈患者和服用乙药的治愈患者中,分别抽取了10名,记录他们的治疗时间(单位:天),统计并绘制了如图2茎叶图,从茎叶图看,哪一种药的疗效更好,并说明理由;
(3)标准差s除了可以用来刻画一组数据的离散程度外,还可以刻画每个数据偏离平均水平的程度,如果出现了治疗时间在(![]() 3s,
3s,![]() 3s)之外的患者,就认为病毒有可能发生了变异,需要对该患者进行进一步检查,若某服用甲药的患者已经治疗了26天还未痊愈,请结合(2)中甲药的数据,判断是否应该对该患者进行进一步检查?
3s)之外的患者,就认为病毒有可能发生了变异,需要对该患者进行进一步检查,若某服用甲药的患者已经治疗了26天还未痊愈,请结合(2)中甲药的数据,判断是否应该对该患者进行进一步检查?
参考公式:s![]() ,
,
参考数据:![]() 48.
48.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络营销和电子商务的兴起,人们的购物方式更具多样化,某调查机构随机抽取10名购物者进行采访,5名男性购物者中有3名倾向于选择网购,2名倾向于选择实体店,5名女性购物者中有2名倾向于选择网购,3名倾向于选择实体店.
(1)若从10名购物者中随机抽取2名,其中男、女各一名,求至少1名倾向于选择实体店的概率;
(2)若从这10名购物者中随机抽取3名,设X表示抽到倾向于选择网购的男性购物者的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 中,角
中,角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,________.是否存在以
,________.是否存在以![]() ,
,![]() ,
,![]() 为边的三角形?如果存在,求出
为边的三角形?如果存在,求出![]() 的面积;若不存在,说明理由.
的面积;若不存在,说明理由.
从①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选一个,补充在上面问题中并作答.
这三个条件中任选一个,补充在上面问题中并作答.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com