
【题目】如图,![]() 是等边三角形,
是等边三角形, ![]() 是
是![]() 边上的动点(含端点),记
边上的动点(含端点),记![]() ,
,![]() .
.

(1)求![]() 的最大值;
的最大值;
(2)若![]() ,求
,求![]() 的面积.
的面积.
科目:高中数学 来源: 题型:
【题目】我国南宋时期著名的数学家秦九韶在其著作《数书九章》中,提出了已知三角形三边长求三角形的面积的公式,与著名的海伦公式完全等价,由此可以看出我国古代已具有很高的数学水平,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂减上,余四约之,为实.一为从隔,开平方得积.”若把以上这段文字写成公式,即 ,其中a、b、c分别为
,其中a、b、c分别为![]() 内角A、B、C的对边.若
内角A、B、C的对边.若![]() ,
,![]() ,则
,则![]() 面积S的最大值为
面积S的最大值为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一名高二学生盼望2020年进入某名牌大学学习,假设该名牌大学有以下条件之一均可录取:①2020年2月通过考试进入国家数学奥赛集训队(集训队从2019年10月省数学竞赛一等奖中选拔):②2020年3月自主招生考试通过并且达到2020年6月高考重点分数线,③2020年6月高考达到该校录取分数线(该校录取分数线高于重点线),该学生具备参加省数学竞赛、自主招生和高考的资格且估计自己通过各种考试的概率如下表
省数学竞赛一等奖 | 自主招生通过 | 高考达重点线 | 高考达该校分数线 |
0.5 | 0.6 | 0.9 | 0.7 |
若该学生数学竞赛获省一等奖,则该学生估计进入国家集训队的概率是0.2.若进入国家集训队,则提前录取,若未被录取,则再按②、③顺序依次录取:前面已经被录取后,不得参加后面的考试或录取.(注:自主招生考试通过且高考达重点线才能录取)
(Ⅰ)求该学生参加自主招生考试的概率;
(Ⅱ)求该学生参加考试的次数![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)求该学生被该校录取的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ax2﹣2ax+1+b(a>0)在区间[0,3]上有最大值4和最小值1.设f(x)=![]() ,
,
(1)求a、b的值;
(2)若不等式f(2x)﹣k2x≥0在x∈[﹣1,1]上有解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设常数![]() .在平面直角坐标系
.在平面直角坐标系![]() 中,已知点
中,已知点![]() ,直线
,直线![]() :
:![]() ,曲线
,曲线![]() :
:![]() .
.![]() 与
与![]() 轴交于点
轴交于点![]() 、与
、与![]() 交于点
交于点![]() .
.![]() 、
、![]() 分别是曲线
分别是曲线![]() 与线段
与线段![]() 上的动点.
上的动点.
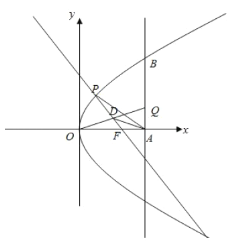
(1)用![]() 表示点
表示点![]() 到点
到点![]() 距离;
距离;
(2)设![]() ,
,![]() ,线段
,线段![]() 的中点在直线
的中点在直线![]() ,求
,求![]() 的面积;
的面积;
(3)设![]() ,是否存在以
,是否存在以![]() 、
、![]() 为邻边的矩形
为邻边的矩形![]() ,使得点
,使得点![]() 在
在![]() 上?若存在,求点
上?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
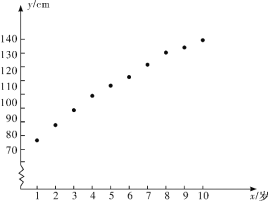
【题目】为了实现绿色发展,避免浪费能源,某市政府计划对居民用电实行阶梯收费的方法.为此,相关部门随机调查了20户居民六月分的月用电量(单位:kwh)和家庭月收入(单位:方元)月用电量数据如下18,63,72,82,93,98,106,10,18,130,134,139,147,163,180,194,212,237,260,324家庭月收入数据如下0.21,0.24,0.35,0.40,0.52,0.60,0.58,0.65,0.65,0.63,0.68,0.80,0.83,0.93,0.97,0.96,1.1,1.2,1.5,1.8
(1)根据国家发改委的指示精神,该市实行3阶阶梯电价,使7%的用户在第一档,电价为0.56元/kwh,20%的用户在第二档,电价为0.61元/kwh,5%的用户在第三档,电价为0.86元/kwh,试求出居民用电费用Q与用电量x间的函数关系式;
(2)以家庭月收入t为横坐标,电量x为纵坐标作出散点图(如图)求出x关于t的回归直线方程(系数四舍五入保留整数);

(3)小明家庭月收入7000元,按上述关系,估计小明家月支出电费多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地1~10岁男童年龄![]() (单位:岁)与身高的中位数
(单位:岁)与身高的中位数![]() (单位
(单位![]() ,如表所示:
,如表所示:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 76.5 | 88.5 | 96.8 | 104.1 | 111.3 | 117.7 | 124 | 130 | 135.4 | 140.2 |
对上表的数据作初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
112.45 | 82.50 | 3947.71 | 566.85 |
(1)求![]() 关于
关于![]() 的线性回归方程(回归方程系数精确到0.01);
的线性回归方程(回归方程系数精确到0.01);
(2)某同学认为方程![]() 更适合作为
更适合作为![]() 关于
关于![]() 的回归方程模型,他求得的回归方程是
的回归方程模型,他求得的回归方程是![]() .经调查,该地11岁男童身高的中位数为
.经调查,该地11岁男童身高的中位数为![]() ,与(1)中的线性回归方程比较,哪个回归方程的拟合效果更好?
,与(1)中的线性回归方程比较,哪个回归方程的拟合效果更好?
(3)从6岁~10岁男童中每个年龄阶段各挑选一位男童参加表演(假设该年龄段身高的中位数就是该男童的身高).再从这5位男童中任挑选两人表演“二重唱”,则“二重唱”男童身高满足![]() 的概率是多少?
的概率是多少?
参考公式: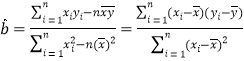 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)的导函数f′(x)的图像如图所示,则下列结论正确的是( )
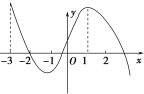
A.f(x)在(-3,-1)上先增后减B.x=-2是f(x)极小值点
C.f(x)在(-1,1)上是增函数D.x=1是函数f(x)的极大值点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际象棋比赛中.胜局一得1分,平一局得0.5分,负一局得0分。今有8名选手进行单循环比赛(每两人均赛一局),赛完后、发现各选手的得分均不相同,当按得分由大到小排列好名次后,第四名选手得4.5分,第二名的得分等于最后四名选手得分总和.问前三名选手各得多少分?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com