已知数列{an}中,a1=1,a2=2,an+1=2an+3an-1(n≥2且n∈N*).
(I)证明数列{an+an+1}是等比数列;
(II)求a1+a2+…an(n∈N*)
解:(I)证明:因为a
n+1=2a
n+3a
n-1,所以a
n+1+a
n=3(a
n+a
n-1),
所以

=3是常数,
所以数列{a
n+a
n+1}是以a
1+a
2=3为首项,等比为3的等比数列;
(II)由(Ⅰ)得a
n+1+a
n=3
n,…①,
又a
n+1=2a
n+3a
n-1(n≥2且n∈N
*).
得a
n+1-3a
n=-(a
n-3a
n-1),(n≥2且n∈N
*).
即
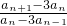
=-1,常数,
所以数列{a
n+1-3a
n}是以-1为首项,公比为-1的等比数列,
a
n+1-3a
n=(-1)
n,…②,
解①②得,a
n=

,
∴a
1+a
2+…a
n=

(3
1+3
2+3
3+…+3
n)-

[(-1)+(-1)
2+(-1)
3+…+(-1)
n]
=

(n∈N
*).
分析:(I)利用a
1=1,a
2=2,a
n+1=2a
n+3a
n-1,推出

是常数,即可证明数列{a
n+a
n+1}是等比数列;
(II)利用(I)推出a
n+1+a
n=3
n,然后说明数列{a
n+1-3a
n}是以-1为首项,公比为-1的等比数列,求出a
n+1-3a
n=(-1)
n,解出a
n,然后求a
1+a
2+…a
n(n∈N
*)
点评:本题考查等比数列的判断,数列通项公式的求法,考查转化思想,计算能力.

 =3是常数,
=3是常数,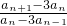 =-1,常数,
=-1,常数, ,
, (31+32+33+…+3n)-
(31+32+33+…+3n)- [(-1)+(-1)2+(-1)3+…+(-1)n]
[(-1)+(-1)2+(-1)3+…+(-1)n] (n∈N*).
(n∈N*). 是常数,即可证明数列{an+an+1}是等比数列;
是常数,即可证明数列{an+an+1}是等比数列;
