
【题目】已知等差数列{an}的公差d>0,设{an}的前n项和为Sn , a1=1,S2S3=36.
(1)求d及Sn;
(2)求m,k(m,k∈N*)的值,使得am+am+1+am+2+…+am+k=65.
【答案】
(1)解:由a1=1,S2S3=36得,
(a1+a2)(a1+a2+a3)=36,
即(2+d)(3+3d)=36,化为d2+3d﹣10=0,
解得d=2或﹣5,
又公差d>0,则d=2,
所以Sn=n ![]() =n2(n∈N*).
=n2(n∈N*).
(2)解:由(1)得,an=1+2(n﹣1)=2n﹣1,
由am+am+1+am+2+…+am+k=65得, ![]() ,
,
即(k+1)(2m+k﹣1)=65,
又m,k∈N*,则(k+1)(2m+k﹣1)=5×13,或(k+1)(2m+k﹣1)=1×65,
下面分类求解:
当k+1=5时,2m+k﹣1=13,解得k=4,m=5;
当k+1=13时,2m+k﹣1=5,解得k=12,m=﹣3,故舍去;
当k+1=1时,2m+k﹣1=65,解得k=0,故舍去;
当k+1=65时,2m+k﹣1=1,解得k=64,m=﹣31,故舍去;
综上得,k=4,m=5.
【解析】(1)根据等差数列通项公式和前n项和公式,把条件转化为关于公差d的二次方程求解,注意d的范围对方程的根进行取舍;(2)由(1)求出等差数列{an}的通项公式,利用等差数列的前n项和公式,对am+am+1+am+2+…+am+k=65化简,列出关于m、k的方程,再由m,k∈N*进行分类讨论,求出符合条件的m、k的值.
【考点精析】关于本题考查的等差数列的前n项和公式和数列的前n项和,需要了解前n项和公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系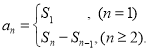 才能得出正确答案.
才能得出正确答案.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() :
: ![]() 与
与![]() 轴的交点是椭圆
轴的交点是椭圆![]() :
: ![]() 的一个焦点.
的一个焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,是否存在
两点,是否存在![]() 使得以线段
使得以线段![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学上、下午各测试一个项目,且不重复.若上午不测“握力”项目,下午不测“台阶”项目,其余项目上、下午都各测试一人,则不同的安排方式共有__________种(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年来,我国许多地区经常出现干旱现象,为抗旱经常要进行人工降雨,现由天气预报得知,某地在未来5天的指定时间的降雨概率是:前3天均为![]() ,后2天均为
,后2天均为![]() ,5天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.
,5天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.
(1)求至少有1天需要人工降雨的概率;
(2)求不需要人工降雨的天数![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四边形ABCD中, ![]() =(3,2),
=(3,2), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3)
=(﹣2,﹣3)
(1)若 ![]() ∥
∥ ![]() ,试求x与y满足的关系式;
,试求x与y满足的关系式;
(2)满足(1)同时又有 ![]() ⊥
⊥ ![]() ,求x,y的值及四边形ABCD的面积.
,求x,y的值及四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=ax+lnx,其中a为常数,设e为自然对数的底数.
(1)当a=-1时,求![]() 的最大值;
的最大值;
(2)若f(x)在区间(0,e]上的最大值为-3,求a的值;
(3)当a=-1时,试推断方程![]() 是否有实数解 .
是否有实数解 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人玩数字游戏,先由甲任想一个数字记为a,再由乙猜甲刚才想的数字,把乙想的数字记为b,且a,b∈{1,2,3,4,5,6},记ξ=|a﹣b|.
(1)求ξ=1的概率;
(2)若ξ≤1,则称“甲乙心有灵犀”,求“甲乙心有灵犀”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com