
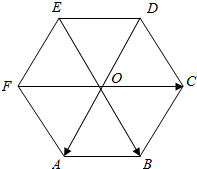
 如图所示.O是正六边形ABCDEF的中心,且$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$.
如图所示.O是正六边形ABCDEF的中心,且$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$.分析 由正六边形的性质和向量的基本概念逐个列举可得.
解答 解:(1)由正六边形的性质可知图中所有的向量都和$\overrightarrow{a}$的模相等,
∴与$\overrightarrow{a}$的模相等的向量有23个;
(2)与$\overrightarrow{a}$的长度相等但方向相反的向量有:$\overrightarrow{AO}$,$\overrightarrow{OD}$,$\overrightarrow{BC}$,$\overrightarrow{FE}$共4个;
(3)与$\overrightarrow{a}$共线的向量有:$\overrightarrow{AO}$,$\overrightarrow{OD}$,$\overrightarrow{BC}$,$\overrightarrow{FE}$,$\overrightarrow{OA}$,$\overrightarrow{DO}$,$\overrightarrow{CB}$,$\overrightarrow{EF}$,$\overrightarrow{AD}$,$\overrightarrow{DA}$共10个;
(4)与$\overrightarrow{a}$相等的向量有:$\overrightarrow{DO}$,$\overrightarrow{CB}$,$\overrightarrow{EF}$共3个;
与$\overrightarrow{b}$相等的向量有:$\overrightarrow{EO}$,$\overrightarrow{FA}$,$\overrightarrow{DC}$共3个;
与$\overrightarrow{c}$相等的向量有:$\overrightarrow{FO}$,$\overrightarrow{AB}$,$\overrightarrow{ED}$共3个.
点评 本题考查向量的基本概念,数形结合并列举是解决问题的关键,属基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$≤a<0 | B. | a≤-$\frac{1}{4}$ | C. | -1≤a≤-$\frac{1}{4}$ | D. | a≤-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com