
【题目】某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖励金额y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:![]() ,
,![]() ,
,![]() ,其中哪个模型能符合公司的要求?
,其中哪个模型能符合公司的要求?
【答案】模型![]() 确实能符合公司要求.
确实能符合公司要求.
【解析】
画出函数图像,根据图像得到模型![]() 进行奖励时才符合公司的要求,得到答案.
进行奖励时才符合公司的要求,得到答案.
作出函数![]() ,
,![]() ,
,![]() ,
,![]() 的图像
的图像
观察图像发现,在区间![]() 上,模型
上,模型![]() ,
,![]() 的图像都有一部分在直线
的图像都有一部分在直线![]() 的上方,只有模型
的上方,只有模型![]() 的图像始终在
的图像始终在![]() 的下方,
的下方,
这说明只有按模型![]() 进行奖励时才符合公司的要求.下面通过计算确认上述判断.
进行奖励时才符合公司的要求.下面通过计算确认上述判断.
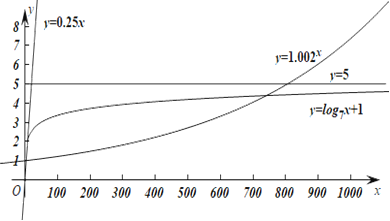
首先计算每个模型的奖金总数不超过5万元.
对于模型![]() ,它在区间
,它在区间![]() 上递增,而且当
上递增,而且当![]() 时,
时,![]() ,因此,当
,因此,当![]() 时,
时,![]() ,所以该模型不符合要求;
,所以该模型不符合要求;
对于模型![]() ,由函数图像,并利用计算器,可知在区间
,由函数图像,并利用计算器,可知在区间![]() 内有一个点
内有一个点![]() 满足
满足![]() ,由于它在区间
,由于它在区间![]() 上递增,因此当
上递增,因此当![]() 时,
时,![]() ,所以该模型也不符合要求;
,所以该模型也不符合要求;
对于模型![]() ,它在区间
,它在区间![]() 上递增,而且当
上递增,而且当![]() 时,
时,![]() ,所以它符合奖金总数不超过5万元的要求.
,所以它符合奖金总数不超过5万元的要求.
再计算按模型![]() 奖励时,奖金是否不超过利润的25%,即当
奖励时,奖金是否不超过利润的25%,即当![]() 时,是否有
时,是否有![]() 成立.
成立.
令![]() ,
,![]() .
.
作出函数![]() 的图像,由图像可知它是递减的,
的图像,由图像可知它是递减的,
因此![]() ,即
,即![]() .
.
所以,当![]() 时,
时,![]() .
.
说明按模型![]() 奖励,奖金不会超过利润的25%.
奖励,奖金不会超过利润的25%.
综上所述,模型![]() 确实能符合公司要求.
确实能符合公司要求.


科目:高中数学 来源: 题型:
【题目】某种设备随着使用年限的增加,每年的维护费相应增加![]() 现对一批该设备进行调查,得到这批设备自购入使用之日起,前五年平均每台设备每年的维护费用大致如表:
现对一批该设备进行调查,得到这批设备自购入使用之日起,前五年平均每台设备每年的维护费用大致如表:
年份 | 1 | 2 | 3 | 4 | 5 |
维护费 |
|
|
|
|
|
![]() Ⅰ
Ⅰ![]() 求y关于t的线性回归方程;
求y关于t的线性回归方程;
![]() Ⅱ
Ⅱ![]() 若该设备的价格是每台5万元,甲认为应该使用满五年换一次设备,而乙则认为应该使用满十年换一次设备,你认为甲和乙谁更有道理?并说明理由.
若该设备的价格是每台5万元,甲认为应该使用满五年换一次设备,而乙则认为应该使用满十年换一次设备,你认为甲和乙谁更有道理?并说明理由.
![]() 参考公式:
参考公式: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() (
(![]() 为常数).
为常数).
(1)若函数![]() 与函数
与函数![]() 在
在![]() 处有相同的切线,求实数
处有相同的切线,求实数![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,证明:
,证明: ![]() ;
;
(3)若对任意![]() ,不等式恒
,不等式恒![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(x0,y0)(x0≠![]() )在椭圆C:
)在椭圆C:![]() (a>b>0)上,若点M为椭圆C的右顶点,且PO⊥PM (O为坐标原点),则椭圆C的离心率e的取值范围是
(a>b>0)上,若点M为椭圆C的右顶点,且PO⊥PM (O为坐标原点),则椭圆C的离心率e的取值范围是
A. (0,![]() ) B. (0,1) C. (
) B. (0,1) C. (![]() ,1) D. (0,
,1) D. (0,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
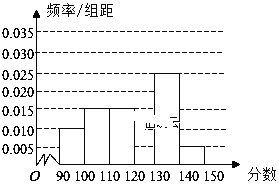
【题目】某校从参加高三模拟考试的学生中随机抽取![]() 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段![]() 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求分数在![]() 内的频率,补全这个频率分布直方图,并据此估计本次考试的平均分;
内的频率,补全这个频率分布直方图,并据此估计本次考试的平均分;
(2)用分层抽样的方法,在分数段为![]() 的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段
的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段![]() 内的概率
内的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知直线
中,已知直线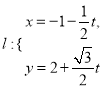 (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立坐标系.
轴的正半轴为极轴建立坐标系.
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的极坐标方程;
的极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设动圆P(圆心为P)经过定点(0,2)、(t+2,0)、(t-2,0)三点,当t变化时,P的轨迹为曲线C
(1) 求C的方程
(2) 过点(0,2)且不垂直于坐标轴的直线l与C交于A、B两点,B点关于y轴的对称点为D,求证:直线AD经过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用红、黄、蓝三种不同颜色给图中的![]() 个矩形随机涂色,每个矩形只涂一种颜色,则
个矩形随机涂色,每个矩形只涂一种颜色,则![]() 个矩形颜色都相同的概率是________,
个矩形颜色都相同的概率是________,![]() 个矩形颜色都不同的概率是________.
个矩形颜色都不同的概率是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com