[题目]已知函数f(x)=2|x+a|+|x﹣ |．(1)当a=1时.解不等式f(x)＜4,+f(﹣x)的最小值．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知函数f（x）=2|x+a|+|x﹣ |（a≠0）．
（1）当a=1时，解不等式f（x）＜4；
（2）求函数g（x）=f（x）+f（﹣x）的最小值．

【答案】
（1）解：∵a=1，∴原不等式为2|x+1|+|x﹣1|＜4，

∴ ，或，或

解得或﹣1≤x＜1或无解，

∴原不等式的解集为

（2）解：g（x）=f（x）+f（﹣x）=

，

当且仅当，即，且（x+a）（x﹣a）＜0，（x+ ）（x﹣ ）＜0时取等号，

∴g（x）的最小值为

【解析】（1）对x的范围进行讨论，去绝对值符号解出；（2）利用绝对值不等式的性质和基本不等式得出最小值．
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识，掌握含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】在平面直角坐标系中，直线l的参数方程为（其中t为参数），现以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C的极坐标方程为ρ=4cosθ．
（Ⅰ）写出直线l和曲线C的普通方程；
（Ⅱ）已知点P为曲线C上的动点，求P到直线l的距离的最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，三棱柱ABC﹣A1B1C1中，侧面BB1C1C为菱形，AB⊥B1C．
（Ⅰ）证明：AC=AB1；
（Ⅱ）若AC⊥AB1 ， ∠CBB1=60°，AB=BC，求二面角A﹣A1B1﹣C1的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知某产品的广告费用x（单位：万元）与销售额y（单位：万元）具有线性关系关系，其统计数据如下表：

x	3	4	5	6
y	25	30	40	45

由上表可得线性回归方程 = x+ ，据此模型预报广告费用为8万元时的销售额是（）
附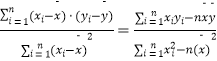： = ； = ﹣ x．
A.59.5
B.52.5
C.56
D.63.5

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】网购是当前民众购物的新方式，某公司为改进营销方式，随机调查了100名市民，统计其周平均网购的次数，并整理得到如下的频数分布直方图．这100名市民中，年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷，且已知其中有5名市民的年龄超过40岁．
（1）根据已知条件完成下面的2×2列联表，能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关？