
【题目】已知点![]() ,
,![]() 是函数
是函数![]()
![]() 图象上的任意两点,且角
图象上的任意两点,且角![]() 的终边经过点
的终边经过点![]() ,若
,若![]() 时,
时,![]() 的 最小值为
的 最小值为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)利用三角函数的定义求出![]() 的值,由
的值,由![]() 时,
时,![]() 的最小值为
的最小值为![]() ,可得函数的周期,从而可求
,可得函数的周期,从而可求![]() ,进而可求函数
,进而可求函数![]() 的解析式;(2)当
的解析式;(2)当![]() 时,不等式
时,不等式![]() 恒成立,等价于
恒成立,等价于![]() ,先求出得
,先求出得![]() 的最大值,由此可得
的最大值,由此可得![]() 的取值范围.
的取值范围.
试题解析:(1)角![]() 的终边经过点
的终边经过点![]() ,
,![]() ,
,
![]() ,
,![]() .
.
由![]() 时,
时,![]() 的最小值为
的最小值为![]() ,得
,得![]() ,即
,即![]() ,
,
![]() ∴
∴![]()
(2)当![]() 时,
时,![]() , 于是,
, 于是,![]() ,
,![]()
等价于![]()
由 ![]() , 得
, 得![]() 的最大值为
的最大值为![]()
所以,实数![]() 的取值范围是
的取值范围是![]()
注:用别的方法求得![]() ,只要正确就给3分.
,只要正确就给3分.
【方法点晴】本题主要考查三角函数图像与性质及不等式恒成立问题,属于难题.不等式恒成立问题常见方法:① 分离参数![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立(
恒成立(![]() 即可);② 数形结合(
即可);② 数形结合(![]() 图象在
图象在![]() 上方即可);③ 讨论最值
上方即可);③ 讨论最值![]() 或
或![]() 恒成立;④ 讨论参数.本题是利用方法 ① 求得
恒成立;④ 讨论参数.本题是利用方法 ① 求得![]() 的范围的.
的范围的.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,以坐标原点为极点,![]() 轴为正半轴建立极坐标系,圆
轴为正半轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为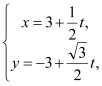 (t为参数).
(t为参数).
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)求直线![]() 分圆
分圆![]() 所得的两弧程度之比.
所得的两弧程度之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某飞机失联,经卫星侦查,其最后出现在小岛![]() 附近,现派出四艘搜救船
附近,现派出四艘搜救船![]() ,为方便联络,船
,为方便联络,船![]() 始终在以小岛
始终在以小岛![]() 为圆心,100海里为半径的圆上,船
为圆心,100海里为半径的圆上,船![]() 构成正方形编队展开搜索,小岛
构成正方形编队展开搜索,小岛![]() 在正方形编队外(如图).设小岛
在正方形编队外(如图).设小岛![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() ,
,![]() 船到小岛
船到小岛![]() 的距离为
的距离为![]() .
.
(1)请分别求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ,并分别写出定义域;
,并分别写出定义域;
(2)当![]() 两艘船之间的距离是多少时搜救范围最大(即
两艘船之间的距离是多少时搜救范围最大(即![]() 最大)?
最大)?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了普及法律知识,达到“法在心中”的目的,某市法制办组织了普法知识竞赛.统计局调查队随机抽取了甲、乙两单位中各5名职工的成绩,成绩如下表:
甲单位 | 87 | 88 | 91 | 91 | 93 |
乙单位 | 85 | 89 | 91 | 92 | 93 |
(1)根据表中的数据,分别求出甲、乙两单位职工成绩的平均数和方差,并判断哪个单位对法律知识的掌握更稳定;
(2)用简单随机抽样法从乙单位5名职工中抽取2名,他们的成绩组成一个样本,求抽取的2名职工的分数差至少是4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
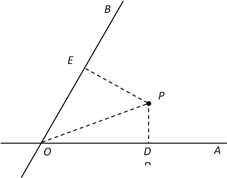
【题目】如图,![]() 、
、![]() 是两条公路(近似看成两条直线),
是两条公路(近似看成两条直线),![]() ,在
,在![]() 内有一纪念塔
内有一纪念塔![]() (大小忽略不计),已知
(大小忽略不计),已知![]() 到直线
到直线![]() 、
、![]() 的距离分别为
的距离分别为![]() 、
、![]() ,
,![]() =6千米,
=6千米,![]() =12千米.现经过纪念塔
=12千米.现经过纪念塔![]() 修建一条直线型小路,与两条公路
修建一条直线型小路,与两条公路![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() .
.
(1)求纪念塔![]() 到两条公路交点
到两条公路交点![]() 处的距离;
处的距离;
(2)若纪念塔![]() 为小路
为小路![]() 的中点,求小路
的中点,求小路![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() (
(![]() ).
).
(1)证明:直线![]() 过定点;
过定点;
(2)若直线不经过第四象限,求![]() 的取值范围;
的取值范围;
(3)若直线![]() 轴负半轴于
轴负半轴于![]() ,交
,交![]() 轴正半轴于
轴正半轴于![]() ,△
,△![]() 的面积为
的面积为![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的最小值,并求此时直线
的最小值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com