
(本小题9分)
如图所示,在直角梯形ABCP中,AB=BC=3,AP=7,CD⊥AP,现将 沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
(I)求证:PA//平面EFG;
(II)若M为线段CD上的一个动点,问当M在什么位置时,MF与平面EFG所成角最大。
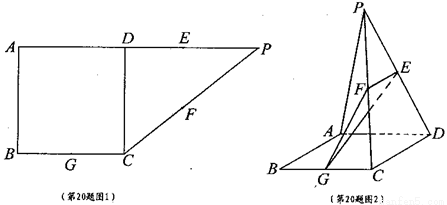
(I)证明见解析。
(II)M为线段CD中点时 ,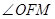 最大。
最大。
【解析】方法一:
(I)证明: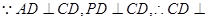 平面PAD,
平面PAD,
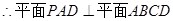 2分
2分
过P作AD的垂线,垂足为O,则PO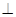 平面ABCD。
平面ABCD。
过O作BC的垂线,交BC于H,以OH,OD,OP为x
轴,y轴,z轴建立空间直角坐标系,
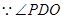 是二面角P—PC—A的平面角,
是二面角P—PC—A的平面角,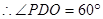 ,
,
又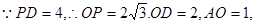
得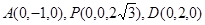
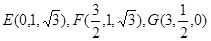
故 4分
4分
设平面EFG的一个法向量为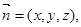 则
则
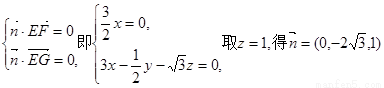 6分
6分
而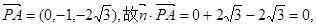
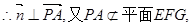 故PA//平面EFG。 7分
故PA//平面EFG。 7分
(II)解:设M(x,2,0),则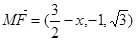 , 9分
, 9分
设MF与平面EFG所成角为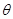 ,
,
则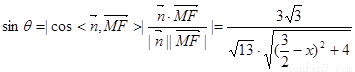 12分
12分
故当 取到最大值,则
取到最大值,则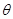 取到最大值,此时点M为线段CD的中点。14分
取到最大值,此时点M为线段CD的中点。14分
方法二:
(I)证明:取AD的中点H,连结EH,HG。 2分
 H,G为AD,BC的中点,∴HG//CD,又EF//CD。
H,G为AD,BC的中点,∴HG//CD,又EF//CD。
∴EF//HG,
∴E,F,G,H四点共面
又∵PA//EH,EH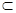 平面EFGH,PA
平面EFGH,PA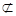 平面EFGH,
平面EFGH,
∴PA//平面EFG。 7分
(II)解:过M作MO⊥平面EFG,垂足O,连结OF,
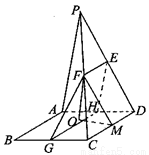
则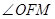 即为MF与平面EFG所成角,因为CD//EF,
即为MF与平面EFG所成角,因为CD//EF,
故CD//平面EFG,故CD上的点M到平面EFG的距离
MO为定长,故要使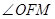 最大,只要MF最短,故当
最大,只要MF最短,故当
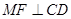 时,即M为线段CD中点时 ,
时,即M为线段CD中点时 ,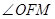 最大。
最大。


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
(本小题13分)
测量地震级别的里氏是地震强度(即地震释放的能量)的常用对数值,显然级别越高,地震的强度也越高。如日本1923年地震为8.9级,旧金山1906年地震是8.3级,1989年地震为7.1级。试计算一下日本1923年地震强度是8.3级的几倍?是7.1级的几倍?(取lg2=0.3)
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高二上期中考试理科数学试卷(解析版) 题型:解答题
(本小题9分)如图是一个空间几何体的三视图,其正视图与侧视图是边长为4cm的正三角形、俯视图中正方形的边长为4cm,
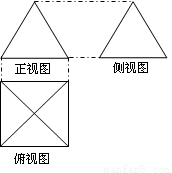
(1)画出这个几何体的直观图(不用写作图步骤);
(2)请写出这个几何体的名称,并指出它的高是多少;
(3)求出这个几何体的表面积。
查看答案和解析>>
科目:高中数学 来源:2013届福建省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
(本小题9分)
如图,四棱锥S—ABCD的底面是正方形,SD 平面ABCD,SD=2a,
平面ABCD,SD=2a, ,点E是SD上的点,且
,点E是SD上的点,且

(Ⅰ)求证:对任意的 ,都有
,都有
(Ⅱ)设二面角C—AE—D的大小为
 ,直线BE与平面ABCD所成的角为
,直线BE与平面ABCD所成的角为 ,若
,若 ,求
,求 的值
的值
查看答案和解析>>
科目:高中数学 来源:2010年北京市高一下学期期末考试数学卷 题型:解答题
(本小题9分)如图:已知圆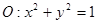 和定点
和定点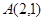 ,由圆
,由圆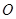 外一点
外一点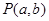 向圆
向圆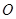 引切线
引切线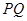 ,切点为
,切点为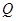 ,且满足
,且满足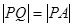
(1)求实数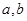 间满足的等量关系;(2)求线段
间满足的等量关系;(2)求线段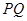 长的最小值;(3)若以
长的最小值;(3)若以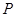 为圆心所作的圆
为圆心所作的圆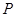 与圆
与圆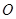 有公共点,试求半径最小时圆
有公共点,试求半径最小时圆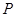 的方程
的方程
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com