已知函数f(x)=ax2+2lnx.
(1)求f(x)的单调区间;
(2)若f(x)在(0,1]上的最大值是-2,求a的值;
(3)记g(x)=f(x)+(a-1)lnx+1,当a≤-2时,求证:对任意x1,x2∈(0,+∞),总有|g(x1)-g(x2)|≥4|x1-x2|
解析:(1)f(x)的定义域是(0,+∞).
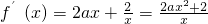
.
当a≥0时,f
′(x)>0,故f(x)在(0,+∞)上是增函数;
当a<0时,令f
′(x)=0,则2ax
2+2=0,所以,
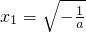
,
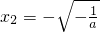
(舍去).
当
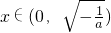
时,f
′(x)>0,故f(x)在
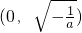
上是增函数;
当
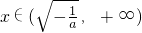
时,f
′(x)<0,故f(x)在
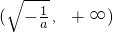
上是减函数.
故当a≥0时,f(x)的增区间是(0,+∞);
当a<0时,f(x)的增区间是
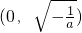
,减区间是
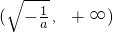
.
(2)①当a≥0时,f(x)在(0,+∞)上是增函数,故在(0,1]上的最大值为f(1)=a+2ln1=a=-2,显然不合题意;
②若
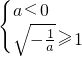
,即-1≤a<0时,(0,1]⊆
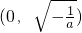
,则f(x)在(0,1]上是增函数,故在(0,1]上最大值为f(1)=a=-2,不合题意,舍去;
③若
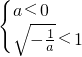
,即a<-1时,f(x)在
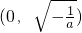
上是增函数,在
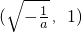
上为减函数,故在(0,1]上的最大值是
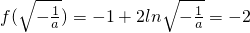
,解得:a=-e,符合.
综合①、②、③得:a=-e.
(3)由g(x)=f(x)+(a-1)lnx+1,则g(x)=(a+1)lnx+ax
2+1,
则
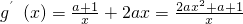
,当a≤-2时,g
′(x)<0,故当a≤-2时,g(x)在(0,+∞)上为减函数.
不妨设x
2≥x
1>0,则g(x
2)≤g(x
1),故|g(x
1)-g(x
2)|≥4|x
1-x
2|等价于g(x
1)-g(x
2)≥4(x
2-x
1),
即g(x
1)+4x
1≥g(x
2)+4x
2.
记h(x)=g(x)+4x,下面证明当x
2≥x
1>0时,h(x
1)≥h(x
2)
由h(x)=g(x)+4x=(a+1)lnx+ax
2+4x+1得:
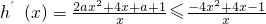
=
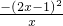
≤0,
从而h(x)在(0,+∞)上为减函数,故当x
2≥x
1>0时,h(x
1)>h(x
2),
即有:g(x
1)+4x
1≥g(x
2)+4x
2,
故当a≤-2时,对任意x
1,x
2∈(0,+∞),总有|g(x
1)-g(x
2)|≥4|x
1-x
2|.
分析:(1)求出函数的导函数,对a≥0和a<0进行分类,当a≥0时,导函数恒大于0,当a<0时,由导函数的零点对定义域分段,根据导函数在各区间段内的符号,判断出原函数的单调性;
(2)根据(1)中求出的单调区间,判断出函数在(0,1]上的单调性,进一步求出函数在(0,1]上的最大值,由最大值等于-2求解a的值,符合条件保留,否则舍去;
(3)把函数f(x)的解析式代入g(x)=f(x)+(a-1)lnx+1,求出函数g(x)的导函数后,由a≤-2可知其导函数小于0,得到函数g(x)为定义域上的减函数,不妨规定x
1和x
2的大小,把要证的不等式取绝对值移向变形,使问题转化成证明一个函数的单调性问题,最后利用函数的导函数证明函数单调性.
点评:本题考查了利用导数研究函数的单调性,利用函数的导函数分析函数在闭区间上的最值,考查了分类讨论的数学思想和数学转化思想,在(3)的证明过程中,构造函数是该题的难点.属难度较大的题目.

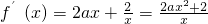 .
.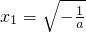 ,
,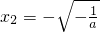 (舍去).
(舍去).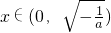 时,f′(x)>0,故f(x)在
时,f′(x)>0,故f(x)在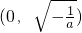 上是增函数;
上是增函数;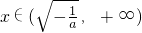 时,f′(x)<0,故f(x)在
时,f′(x)<0,故f(x)在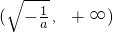 上是减函数.
上是减函数.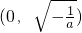 ,减区间是
,减区间是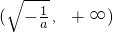 .
.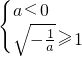 ,即-1≤a<0时,(0,1]⊆
,即-1≤a<0时,(0,1]⊆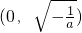 ,则f(x)在(0,1]上是增函数,故在(0,1]上最大值为f(1)=a=-2,不合题意,舍去;
,则f(x)在(0,1]上是增函数,故在(0,1]上最大值为f(1)=a=-2,不合题意,舍去;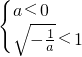 ,即a<-1时,f(x)在
,即a<-1时,f(x)在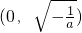 上是增函数,在
上是增函数,在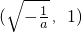 上为减函数,故在(0,1]上的最大值是
上为减函数,故在(0,1]上的最大值是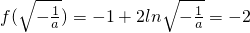 ,解得:a=-e,符合.
,解得:a=-e,符合.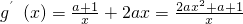 ,当a≤-2时,g′(x)<0,故当a≤-2时,g(x)在(0,+∞)上为减函数.
,当a≤-2时,g′(x)<0,故当a≤-2时,g(x)在(0,+∞)上为减函数.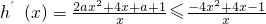 =
=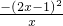 ≤0,
≤0,
