
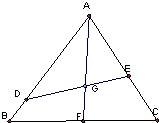
 如图,已知点G是边长为1的正三角形ABC的中心,线段DE经过点G,并绕点G转动,分别交边AB、AC于点D、E;设
如图,已知点G是边长为1的正三角形ABC的中心,线段DE经过点G,并绕点G转动,分别交边AB、AC于点D、E;设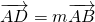 ,
,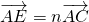 ,其中0<m≤1,0<n≤1.
,其中0<m≤1,0<n≤1. 的值,并说明理由;
的值,并说明理由;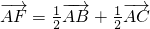
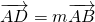 ,
,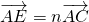 ,
,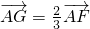
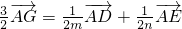 即
即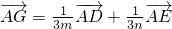
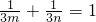
 =3
=3 (2)∵△ABC是边长为1的正三角形,
(2)∵△ABC是边长为1的正三角形, mn
mn =3,0<m≤1,0<n≤1
=3,0<m≤1,0<n≤1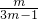 ,
,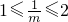 即
即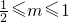 .
. mn=
mn=
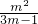
 则m=t+
则m=t+ (
(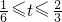 )
) mn=
mn=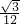 (t+
(t+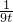 +
+ )
)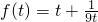 在
在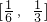 为减函数,在
为减函数,在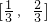 为增函数.
为增函数. ,即
,即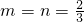 ,时,f(t)取得最小值
,时,f(t)取得最小值 ,
,
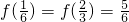 ,
, ,
, ,此时
,此时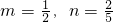 或
或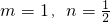
 用向量
用向量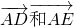 表达,由D、G、E三点共线,即可得到m和n的关系.
表达,由D、G、E三点共线,即可得到m和n的关系. mn,由(1)可知
mn,由(1)可知 =3,由消元法n=
=3,由消元法n=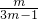 ,转化为m的函数求最值即可.
,转化为m的函数求最值即可.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
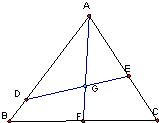 如图,已知点G是边长为1的正三角形ABC的中心,线段DE经过点G,并绕点G转动,分别交边AB、AC于点D、E;设
如图,已知点G是边长为1的正三角形ABC的中心,线段DE经过点G,并绕点G转动,分别交边AB、AC于点D、E;设| AD |
| AB |
| AE |
| AC |
| 1 |
| m |
| 1 |
| n |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年上海市十校高三(上)第一次联考数学试卷(理科)(解析版) 题型:解答题
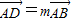 ,
,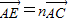 ,其中0<m≤1,0<n≤1.
,其中0<m≤1,0<n≤1.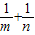 的值,并说明理由;
的值,并说明理由;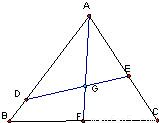
查看答案和解析>>
科目:高中数学 来源:2009-2010学年上海市十校高三(上)第一次联考数学试卷(文科)(解析版) 题型:解答题
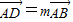 ,
,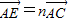 ,其中0<m≤1,0<n≤1.
,其中0<m≤1,0<n≤1.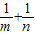 的值,并说明理由;
的值,并说明理由;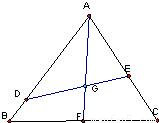
查看答案和解析>>
科目:高中数学 来源:《第2章 平面向量》2010年单元测试卷(2)(解析版) 题型:解答题
 ,
,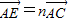 ,其中0<m≤1,0<n≤1.
,其中0<m≤1,0<n≤1.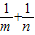 的值,并说明理由;
的值,并说明理由;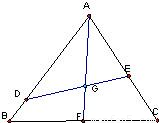
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com