练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

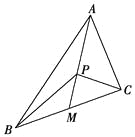
    【题目】在△ABC中，中线长AM＝2.

    （1）若＝－2，求证：＋＋＝0；

    （2）若P为中线AM上的一个动点，求·(＋)的最小值．

    【答案】（1）见解析；（2）最小值－2.

    【解析】

    试题（1） ∵M是BC的中点，∴＝(＋)．代入＝－2，得＝－－，即＋＋＝0

    （2）若P为中线AM上的一个动点，若AM＝2，我们易将·(＋),转化为－2||||=2(x－1)2－2的形式，然后根据二次函数在定区间上的最值的求法，得到答案．

    试题解析：（1）证明：∵M是BC的中点，

    ∴＝(＋)

    代入＝－2，得＝－－，

    即＋＋＝0

    （2）设||＝x，则||＝2－x(0≤x≤2)

    ∵M是BC的中点，∴＋＝2

    ∴·(＋)＝2·＝－2||||

    ＝－2x(2－x)＝2(x2－2x)＝2(x－1)2－2，

    当x＝1时，取最小值－2

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】对函数（其中为实数，），给出下列命题；

    ①当时，在定义域上为单调递减函数；②对任意，都不是奇函数；③当时，为偶函数；④关于的方程最多有一个实数根，其中正确命题的序号为________，（把所有正确的命题序号写入横线）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线的参数方程为 为参数），以原点为极点，以轴正半轴为极轴建立极坐标系，曲线的极坐标方程为，曲线，的公共点为.

    （Ⅰ）求直线的斜率；

    （Ⅱ）若点分别为曲线，上的动点，当取最大值时，求四边形的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f(x)=Asin(wx+j)(A＞0，w＞0，-＜j＜，x∈R)的部分图象如图所示：，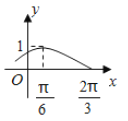

    (1)求函数y=f(x)的解析式；(2)当x∈时，求f(x)的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点A(0，－2)，椭圆E： (a>b>0)的离心率为，F是椭圆E的右焦点，直线AF的斜率为，O为坐标原点.

    (1)求E的方程；

    (2)设过点A的动直线l与E相交于P，Q两点.当△OPQ的面积最大时，求l的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高中为了了解高三学生每天自主参加体育锻炼的情况，随机抽取了100名学生进行调查，其中女生有55名.下面是根据调查结果绘制的学生自主参加体育锻炼时间的频率分布直方图：

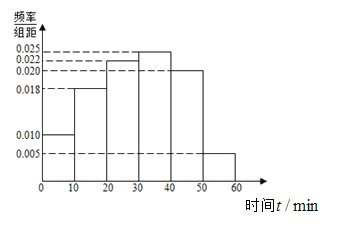
    将每天自主参加体育锻炼时间不低于40分钟的学生称为体育健康A类学生，已知体育健康A类学生中有10名女生.

    （Ⅰ）根据已知条件完成下面列联表，并据此资料你是否认为达到体育健康A类学生与性别有关？

    非体育健康A类学生

    体育健康A类学生

    合计

    男生

    女生

    合计

    （Ⅱ）将每天自主参加体育锻炼时间不低于50分钟的学生称为体育健康类学生，已知体育健康类学生中有2名女生，若从体育健康类学生中任意选取2人，求至少有1名女生的概率.

    附：

    P（）

    0.05

    0.010

    0.005

    3.841

    6.635

    7.879

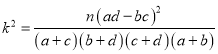
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C的圆心为(1，1)，直线与圆C相切.

    （1）求圆C的标准方程；

    （2）若直线过点(2，3)，且被圆C所截得的弦长为2，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】ΔABC的内角A，B，C的对边分别为a，b，c，根据下列条件解三角形，其中有两解的是

    A. a=2，b=3，A=30°B. b=6，c=4，A=120°

    C. a=4，b=6，A=60°D. a=3，b=6，A=30°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了适应高考改革，某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课，高一平行乙班采用“创新课堂”的教学方式授课，为了比较教学效果，期中考试后，分别从两个班中各随机抽取名学生的成绩进行统计分析，结果如下表：（记成绩不低于分者为“成绩优秀”）

    分数

    甲班频数

    乙班频数

    （1）由以上统计数据填写下面的列联表，并判断是否有以上的把握认为“成绩优秀与教学方式有关”？

    甲班

    乙班

    总计

    成绩优秀

    成绩不优秀

    总计

    （2）在上述样本中，学校从成绩为的学生中随机抽取人进行学习交流，求这人来自同一个班级的概率.

    参考公式：，其中.

    临界值表

    查看答案和解析>>

    同步练习册答案