
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆上.不过原点的直线
在椭圆上.不过原点的直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的方程;
的方程;
(2)试判断![]() 是否为定值?若是,求出这个值;若不是,请说明理由.
是否为定值?若是,求出这个值;若不是,请说明理由.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】有下列说法:
①若某商品的销售量![]() (件)关于销售价格
(件)关于销售价格![]() (元/件)的线性回归方程为
(元/件)的线性回归方程为![]() ,当销售价格为10元时,销售量一定为300件;
,当销售价格为10元时,销售量一定为300件;
②线性回归直线![]() 一定过样本点中心
一定过样本点中心![]() ;
;
③若两个随机变量的线性相关性越强,则相关系数![]() 的值越接近于1;
的值越接近于1;
④在残差图中,残差点比较均匀落在水平的带状区域中即可说明选用的模型比较合适,与带状区域的宽度无关;
⑤在线性回归模型中,相关指数![]() 表示解释变量对于预报变量变化的贡献率,
表示解释变量对于预报变量变化的贡献率,![]() 越接近于1,表示回归的效果越好;
越接近于1,表示回归的效果越好;
其中正确的结论有几个( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,直线l1的参数方程为![]() (t为参数),直线l2的参数方程为
(t为参数),直线l2的参数方程为 .设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
.设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ) ![]() =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出,将冰雪这个冷项目迅速炒“热”.北京某综合大学计划在一年级开设冰球课程,为了解学生对冰球运动的兴趣,随机从该校一年级学生中抽取了100人进行调查,其中女生中对冰球运动有兴趣的占![]() ,而男生有10人表示对冰球运动没有兴趣额.
,而男生有10人表示对冰球运动没有兴趣额.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对冰球是否有兴趣与性别有关”?
的把握认为“对冰球是否有兴趣与性别有关”?
有兴趣 | 没兴趣 | 合计 | |
男 | 55 | ||
女 | |||
合计 |
(2)若将频率视为概率,现再从该校一年级全体学生中,采用随机抽样的方法每次抽取1名学生,抽取5次,记被抽取的5名学生中对冰球有兴趣的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列,期望和方差.
的分布列,期望和方差.
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
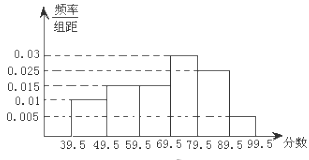
(1)![]() 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率(60分及以上为及格).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x+1)-loga(1-x),a>0且a≠1.
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并予以证明;
(3)当a>1时,求使f(x)>0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】3名男生和3名女生共6人站成一排,若男生甲不站两端,且不与男生乙相邻,3名女生有且只有2名女生相邻,则不同排法的种数是_____.(用数字作答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com