
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使得
折起,使得![]() .
.
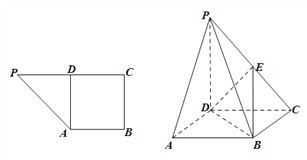
(Ⅰ)若![]() 是
是![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求二面角![]() 的大小.
的大小.
【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析: ![]() 连接
连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,推导出
,推导出![]() ,由此能证明
,由此能证明![]() 平面
平面![]() ;
; ![]() 推导出
推导出![]() ,从而
,从而![]() 平面
平面![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() ;
; ![]() 以
以![]() 为原点,以
为原点,以![]() 所在的直线分别为
所在的直线分别为![]() 轴
轴![]() 轴,
轴, ![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,利用向量法能求出二面角
,利用向量法能求出二面角![]() 的大小
的大小
解析:(Ⅰ)证明:连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
在正方形![]() 中,
中, ![]() 为
为![]() 中点,又因为
中点,又因为![]() 为
为![]() 中点,
中点,
所以![]() ,
,
又因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)由已知可得![]()
又因为![]() 平面
平面![]()
所以![]() 平面
平面![]()
因为![]() 平面
平面![]()
所以平面![]() 平面
平面![]()
解:(Ⅲ)由(Ⅱ)知, ![]() 平面
平面![]() 所以
所以![]() ,又因为
,又因为![]()
所以![]() 平面
平面![]()
所以以![]() 为原点,以
为原点,以![]() 所在的直线分别为
所在的直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,
,
则点![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
所以![]() 即
即![]()
令![]() ,解得
,解得![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
所以![]() 即
即![]()
令![]() ,解得
,解得![]() .
.
所以![]() .
.
由图可知,二面角![]() 为钝角,所以二面角
为钝角,所以二面角![]() 的大小为
的大小为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
| |||||
|
|
| |||
|
(1)请结合所给表格,在所给的坐标系中作出函数![]() 一个周期内的简图;
一个周期内的简图;

(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)求![]() 的最大值和最小值及相应
的最大值和最小值及相应![]() 的取值.
的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1:(x+1)2+(y-3)2=9和圆C2:x2+y2-4x+2y-11=0.
(1)求两圆公共弦所在直线的方程;
(2)求直线过点C(3,-5),且与公共弦垂直的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为[0,1]的函数f(x)同时满足以下三个条件:
①对任意的x∈[0,1],总有f(x)≥0;
②f(1)=1;
③当x1,x2∈[0,1],且x1+x2∈[0,1]时,f(x1+x2)≥f(x1)+f(x2)成立.称这样的函数为“友谊函数”.
请解答下列各题:
(1)已知f(x)为“友谊函数”,求f(0)的值;
(2)函数g(x)=2x-1在区间[0,1]上是否为“友谊函数”?请给出理由;
(3)已知f(x)为“友谊函数”,假定存在x0∈[0,1],使得f(x0)∈[0,1],且f[f(x0)]=x0,求证: f(x0)=x0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集![]() 具有性质
具有性质![]() :对任意的
:对任意的![]()
![]() ,
,![]() ,使得
,使得![]() 成立.
成立.
(Ⅰ)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(Ⅱ)求证![]() ;
;
(Ⅲ)若![]() ,求数集
,求数集![]() 中所有元素的和的最小值.
中所有元素的和的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】节能灯的质量通过其正常使用时间来衡量,使用时间越长,表明质量越好,且使用时间大于或等于6千小时的产品为优质品.现用A,B两种不同型号的节能灯做试验,各随机抽取部分产品作为样本,得到试验结果的频率分布直方图如图所示.
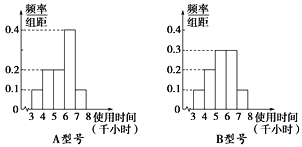
以上述试验结果中使用时间落入各组的频率作为相应的概率.
(1)现从大量的A,B两种型号节能灯中各随机抽取两件产品,求恰有两件是优质品的概率;
(2)已知A型节能灯的生产厂家对使用时间小于6千小时的节能灯实行“三包”.通过多年统计发现,A型节能灯每件产品的利润y(单位:元)与其使用时间t(单位:千小时)的关系如下表:
使用时间t(单位:千小时) | t<4 | 4≤t<6 | t≥6 |
每件产品的利润y(单位:元) | -10 | 10 | 20 |
若从大量的A型节能灯中随机抽取两件,其利润之和记为X(单位:元),求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2019年春运期间十二个城市售出的往返机票的平均价格以及相比去年同期变化幅度的数据统计图,给出下列4个结论
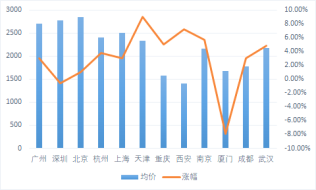
其中结论正确的是( )
A.深圳的变化幅度最小,北京的平均价格最高;
B.深圳和厦门往返机票的平均价格同去年相比有所下降;
C.平均价格从高到低位于前三位的城市为北京,深圳,广州;
D.平均价格的涨幅从高到低位于前三位的城市为天津,西安,上海.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com