
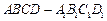 中,底面
中,底面 是直角梯形,
是直角梯形,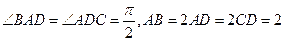
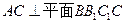
 上是否存一点
上是否存一点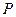 ,使得
,使得 与平面
与平面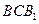 与平面
与平面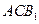 都平行?证明你的结论.
都平行?证明你的结论.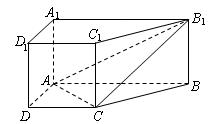
 直棱柱
直棱柱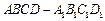 中,
中, BB1⊥平面ABCD,
BB1⊥平面ABCD,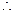 BB1⊥AC.…2分
BB1⊥AC.…2分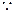 ∠BAD=∠ADC=90°,
∠BAD=∠ADC=90°,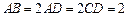 ,
,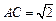 ,∠CAB=45°,
,∠CAB=45°,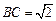 ,
,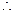 BC⊥AC. ……5分
BC⊥AC. ……5分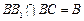 ,
, 平面B
平面B B1C1C,
B1C1C,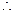 AC⊥平面BB1C1C…7分
AC⊥平面BB1C1C…7分 上是否存一点
上是否存一点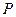 ,使得
,使得 与平面
与平面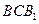 与平面
与平面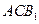 都平行?证明你的结论.
都平行?证明你的结论.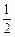 AB.…………9分
AB.…………9分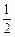 AB,
AB,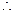 DC∥PB1,且DC= PB1,
DC∥PB1,且DC= PB1,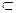 面ACB1,DP
面ACB1,DP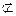 面ACB1,
面ACB1,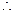 DP∥面ACB1. …………12分
DP∥面ACB1. …………12分 ∥面BCB1. ……………………………………13分
∥面BCB1. ……………………………………13分

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .
.
 SC; (II)求平
SC; (II)求平 面SBC与平面ABCD所成二面角的大小;
面SBC与平面ABCD所成二面角的大小;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 求证:EF⊥平面PCD。
求证:EF⊥平面PCD。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
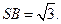
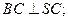
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.不相交的两条直线 | B.分别位于两个平面内的直线 |
| C.一个平面内的直线和不在这个平面内的直线 | D.不同在任何一个平面内的两条直线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com