
【题目】某连锁分店销售某种商品,每件商品的成本为4元,并且每件商品需向总店交![]() 元的管理费,预计当每件商品的售价为
元的管理费,预计当每件商品的售价为![]() 元时,一年的销售量为
元时,一年的销售量为![]() 万件.
万件.
(1)求该连锁分店一年的利润![]() (万元)与每件商品的售价
(万元)与每件商品的售价![]() 的函数关系式
的函数关系式![]() ;
;
(2)当每件商品的售价为多少元时,该连锁分店一年的利润![]() 最大,并求出
最大,并求出![]() 的最大值.
的最大值.
【答案】(I)![]() .
.
(II)当![]() 每件商品的售价为7元时,该连锁分店一年的利润
每件商品的售价为7元时,该连锁分店一年的利润![]() 最大,最大值为
最大,最大值为![]() 万元;
万元;
当![]() 每件商品的售价为
每件商品的售价为![]() 元时,该连锁分店一年的利润
元时,该连锁分店一年的利润![]() 最大,最大值为
最大,最大值为![]() 万元.
万元.
【解析】
试题(1)该连锁分店一年的利润L(万元)与售价x的函数关系式为
L(x)= (x-4-a)(10-x)2,x∈[8,9].
(2)![]() =(10-x)(18+2a-3x),
=(10-x)(18+2a-3x),
令![]() ,得x =6+
,得x =6+![]() a或x=10(舍去).∵1≤a≤3,∴
a或x=10(舍去).∵1≤a≤3,∴![]() ≤6+
≤6+![]() a≤8.
a≤8.
所以L(x)在x∈[8,9]上单调递减,故![]() =L(8)=(8-4-a)(10-8)2=16-4a.
=L(8)=(8-4-a)(10-8)2=16-4a.
即M(a) =16-4a.
答:当每件商品的售价为8元时,该连锁分店一年的利润L最大,
最大值为16-4a万元.


科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了茎叶图:则下列结论中表述不正确的是
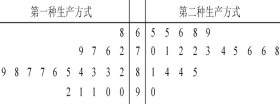
A. 第一种生产方式的工人中,有75%的工人完成生产任务所需要的时间至少80分钟
B. 第二种生产方式比第一种生产方式的效率更高
C. 这40名工人完成任务所需时间的中位数为80
D. 无论哪种生产方式的工人完成生产任务平均所需要的时间都是80分钟.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P是椭圆![]() 上一点,M,N分别是两圆(x+4)2+y2=1和(x-4)2+y2=1上的点,则|PM|+|PN|的最小值、最大值分别为 ( )
上一点,M,N分别是两圆(x+4)2+y2=1和(x-4)2+y2=1上的点,则|PM|+|PN|的最小值、最大值分别为 ( )
A. 9,12 B. 8,11 C. 10,12 D. 8,12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正三角形![]() 的边长为3,
的边长为3,![]() 分别是
分别是![]() 边上的点,满足
边上的点,满足![]() (如图1).将
(如图1).将![]() 折起到
折起到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() ,连接
,连接![]() (如图2).
(如图2).
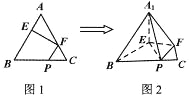
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】邗江中学高二年级某班某小组共10人,利用寒假参加义工活动,已知参加义工活动次数为1,2,3的人数分别为3,3,4.现从这10人中选出2人作为该组代表参加座谈会.
(1)记“选出2人参加义工活动的次数之和为4”为事件![]() ,求事件
,求事件![]() 发生的概率;
发生的概率;
(2)设![]() 为选出2人参加义工活动次数之差的绝对值,求随机变量
为选出2人参加义工活动次数之差的绝对值,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() .数列
.数列![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,且
,且![]() ,求正整数
,求正整数![]() 的值;
的值;
(2)若数列![]() ,
,![]() 均是等差数列,求
均是等差数列,求![]() 的取值范围;
的取值范围;
(3)若数列![]() 是等比数列,公比为
是等比数列,公比为![]() ,且
,且![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() ,
,![]() ,
,![]() 成等差数列,若存在,求出一个
成等差数列,若存在,求出一个![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,直线
,直线![]() 恰好经过椭圆C:
恰好经过椭圆C:![]() 的右顶点和上顶点.
的右顶点和上顶点.
(1)求椭圆C方程;
(2)过椭圆C左焦点F的直线l交椭圆C于![]() 两点,椭圆上存在一点P,使得四边形
两点,椭圆上存在一点P,使得四边形![]() 为平行四边形,求直线l的方程。
为平行四边形,求直线l的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乳业公司生产甲、乙两种产品,需要A,B,C三种苜蓿草饲料,生产1个单位甲种产品和生产1个单位乙种产品所需三种苜蓿草饲料的吨数如下表所示:
产品 苜蓿草饲料 | A | B | C |
甲 | 4 | 8 | 3 |
乙 | 5 | 5 | 10 |
现有A种饲料200吨,B种饲料360吨,C种饲料300吨,在此基础上生产甲乙两种产品,已知生产1个单位甲产品,产生的利润为2万元;生产1个单位乙产品,产生的利润为3万元,分别用x,y表示生产甲、乙两种产品的数量.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲乙两种产品多少时,能够产出最大的利润?并求出此最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com