
求函数y=sin(2x+![]() )的最小正周期及y=|sin(2x+
)的最小正周期及y=|sin(2x+![]() )|的最小正周期.
)|的最小正周期.
|
解:(1)y=sin(2x+ (2)∵f(x+ =|-sin(2x+ ∴T= 假设存在0<T< 令x=0,有|sin( ∵0<T< ∴sin( 从而对任意x应有sin(2x+ 与当x= ∴T= |
|
反证法是证明最小正周期的常用办法,举反例时,只要有一则反例即可.另外,本单元第三节将介绍y=Asin(ωx+φ)的图象,到时可以借助图象直接观察出y=|sin(2x+ |


科目:高中数学 来源:三点一测丛书 高中数学 必修5 (江苏版课标本) 江苏版课标本 题型:044
(1)已知a∈(0,![]() ],求函数y=sinα+
],求函数y=sinα+![]() 最小值;
最小值;
(2)求y=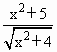 的最小值;
的最小值;
(3)已知函数y=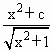 (c>0),求函数的最小值.
(c>0),求函数的最小值.
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修四1.5函数的图象练习卷(一)(解析版) 题型:解答题
设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x= .
.
(1)求φ;
(2)求函数y=f(x)的单调增区间.
查看答案和解析>>
科目:高中数学 来源:2012届江西省南昌市高三第一次模拟测试卷理科数学试卷 题型:填空题
已知向量p=(-cos 2x,a),q=(a,2- sin 2x),函数f(x)=p·q-5(a∈R,a≠0)
sin 2x),函数f(x)=p·q-5(a∈R,a≠0)
(1)求函数f(x)(x∈R)的值域;
(2)当a=2时,若对任意的t∈R,函数y=f(x),x∈(t,t+b]的图像与直线y=-1有且仅有两个不同的交点,试确定b的值(不必证明),并求函数y=f(x)的在[0,b]上单调递增区间.
查看答案和解析>>
科目:高中数学 来源:江西省南昌市2011-2012学年高三下学期第一次模拟测试卷(数学理) 题型:解答题
已知向量p=(-cos 2x,a),q=(a,2-sin 2x),函数f(x)=p·q-5(a∈R,a≠0)
(1)求函数f(x)(x∈R)的值域;
(2)当a=2时,若对任意的t∈R,函数y=f(x),x∈(t,t+b]的图像与直线y=-1有且仅有两个不同的交点,试确定b的值(不必证明),并求函数y=f(x)的在[0,b]上单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com