练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】2019年底，北京2022年冬奥组委会启动志愿者全球招募，仅一个月内报名人数便突破60万，其中青年学生约有50万人.现从这50万青年学生志愿者中，按男女分层抽样随机选取20人进行英语水平测试，所得成绩(单位:分)统计结果用茎叶图记录如下:

    (Ⅰ)试估计在这50万青年学生志愿者中，英语测试成绩在80分以上的女生人数;

    (Ⅱ)从选出的8名男生中随机抽取2人，记其中测试成绩在70分以上的人数为X，求的分布列和数学期望;

    (Ⅲ)为便于联络，现将所有的青年学生志愿者随机分成若干组(每组人数不少于5000)，并在每组中随机选取个人作为联络员，要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据，以频率作为概率，给出的最小值.(结论不要求证明)

    【答案】(Ⅰ)万；(Ⅱ)分布列见解析， ；(Ⅲ)

    【解析】

    (Ⅰ)根据比例关系直接计算得到答案.

    (Ⅱ) 的可能取值为，计算概率得到分布列，再计算数学期望得到答案.

    (Ⅲ) 英语测试成绩在70分以上的概率为 ，故，解得答案.

    (Ⅰ)样本中女生英语成绩在分以上的有人，故人数为：万人.

    (Ⅱ) 8名男生中，测试成绩在70分以上的有人，的可能取值为：.

    ，，.

    故分布列为：

    .

    (Ⅲ) 英语测试成绩在70分以上的概率为 ，故，故.

    故的最小值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】“绿水青山就是金山银山”，为了响应国家政策，我市环保部门对市民进行了一次环境保护知识的网络问卷调查，每位市民仅有一次参加机会，通过随机抽样，得到参与问卷调查的50人的得分（满分：100分）数据，统计结果如表所示：

    组别

    男

    1

    2

    2

    10

    9

    6

    女

    0

    5

    5

    5

    3

    2

    若规定问卷得分不低于70分的市民称为“环境保护关注者”，则上图中表格可得列联表如下：

    非“环境保护关注者”

    是“环境保护关注者”

    合计

    男

    5

    25

    30

    女

    10

    10

    20

    合计

    15

    35

    50

    （1）请完成上述列联表，并判断能否在犯错误的概率不超过0.05的前提下认为“环境保护关注者”与性别有关？

    （2）若问卷得分不低于80分的人称为“环境保护达人”，现在从本次调查的“环境保护达人”中利用分层抽样的方法抽取4名市民参与环保知识问答，再从这4名市民中随机抽取2人参与座谈会，求抽取的2名市民中，既有男“环境保护达人”又有女“环境保护达人”的概率.

    附表及公式：，其中.

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，在等腰梯形中，两腰，底边，，，是的三等分点，是的中点.分别沿，将四边形和折起，使，重合于点，得到如图2所示的几何体.在图2中，，分别为，的中点.

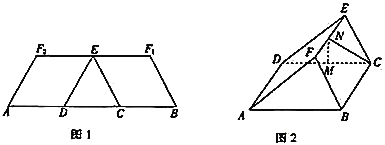
    （1）证明：平面.

    （2）求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现有3名医生，5名护士、2名麻醉师．

    （1）从中选派1名去参加外出学习，有多少种不同的选法？

    （2）从这些人中选出1名医生、1名护士和1名麻醉师组成1个医疗小组，有多少种不同的选法？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两名同学参加一项射击比赛游戏，其中任何一人每射击一次击中目标得2分，未击中目标得0分．若甲、乙两人射击的命中率分别为和，且甲、乙两人各射击一次得分之和为2的概率为．假设甲、乙两人射击互不影响，则值为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝ax2ex﹣1（a≠0）.

    （1）求函数f（x）的单调区间；

    （2）已知a＞0且x∈[1，+∞），若函数f（x）没有零点，求a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校高一年级三个班共有学生120名，这三个班的男女生人数如下表所示，已知在全年级中随机抽取1名学生，抽到二班女生的概率是0.2，则_________.现用分层抽样的方法在全年级抽取30名学生，则应在三班抽取的学生人数为________.

    一班

    二班

    三班

    女生人数

    20

    男生人数

    20

    20

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在区间[0,1]上的函数y＝f(x)的图象如图所示．对满足0<x1<x2<1的任意x1，x2，给出下列结论：

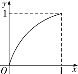
    ①f(x1)－f(x2)>x1－x2；

    ②f(x1)－f(x2)<x1－x2；

    ③x2f(x1)>x1f(x2)；

    ④．

    其中正确结论的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求函数的单调区间；

    （2）若函数在区间上有唯一的极值点，求的取值范围，并证明：.

    查看答案和解析>>

    同步练习册答案