
分析 由条件可得sinβ=$\frac{1}{2}$sinα ①,cosβ=$\frac{3}{2}$cosα ②,或sinα=0 ③.把①、②平方相加即可求得cos2α 的值;由③再得到一个cos2α的值,进而利用二倍角公式可得结论.
解答 解:∵已知sinα=2sinβ,∴sinβ=$\frac{1}{2}$sinα ①.
∵tanα=3tanβ,∴$\frac{sinα}{cosα}$=$\frac{3sinβ}{cosβ}$,可得 cosβ=$\frac{3}{2}$cosα ②,或sinα=0 ③.
若②成立,则把①、②平方相加可得 1=$\frac{1}{4}$sinα2+$\frac{9}{4}$cos2α=$\frac{1}{4}$+2cos2α,
解得 cos2α=$\frac{3}{8}$.可得:cos2α=2cos2α-1=$-\frac{1}{4}$,
若③成立,则有cos2α=1.可得:cos2α=2cos2α-1=1,
综上可得,cos2α=$-\frac{1}{4}$,或cos2α=1.
故答案为:$-\frac{1}{4}$,或1.
点评 本题主要考查三角函数的恒等变换及化简求值,同角三角函数的基本关系,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-2,2] | C. | [-2,1] | D. | [-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.
如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\sqrt{6}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
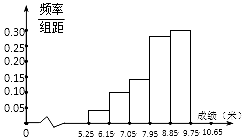 某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com