
已知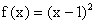 ,
,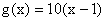 ,数列
,数列 满足
满足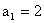 ,
,
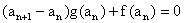 ,
, 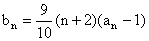 .
.
(I)求证:数列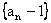 是等比数列;
是等比数列;
(II)当n取何值时,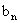 取最大值,并求出最大值;
取最大值,并求出最大值;
(III)若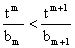 对任意
对任意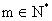 恒成立,求实数
恒成立,求实数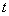 的取值范围.
的取值范围.
解:(I)∵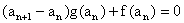 ,
,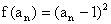 ,
,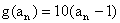 ,
,
∴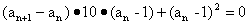 .
.
即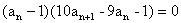 .…………………………………………1分
.…………………………………………1分
又若an≠1,则an+1≠1,事实上当an≠1时,由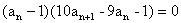 知
知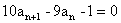 ,若an+1=1,则an=1,从而与an≠1矛盾,故an+1≠1.
,若an+1=1,则an=1,从而与an≠1矛盾,故an+1≠1.
由此及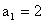 ≠1可知an≠1对任意n∈N
≠1可知an≠1对任意n∈N 都成立.
都成立.
故对任何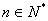 ,
,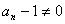 ,………………………………………3分
,………………………………………3分
所以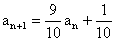 .
.
∵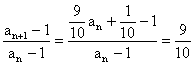 ,
,
∴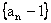 是以
是以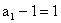 为首项,
为首项,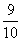 为公比的等比数列.…………5分
为公比的等比数列.…………5分
(II)由(I)可知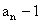 =
=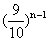 (
( ).
).
∴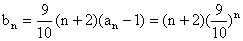 .
.

(III)由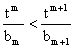 ,得
,得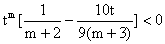 ……………… (*)
……………… (*)
依题意(*)式对任意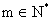 恒成立,
恒成立,
①当t=0时,(*)式显然不成立,因此t=0不符合题意.…………10分
②当t<0时,由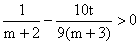 ,可知
,可知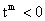 (
(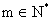 ).
).
而当m是偶数时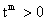 ,因此t<0不符合题意.………………11分
,因此t<0不符合题意.………………11分
③当t>0时,由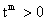 (
(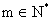 ),
),
∴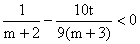 ,∴
,∴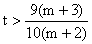 .(
.(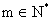 )
)
设 (
(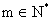 ),
),
∵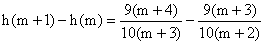 =
=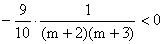 ,
,
∴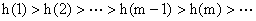 .
.
∴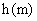 的最大值为
的最大值为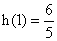 .………………………………13分
.………………………………13分
所以实数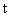 的取值范围是
的取值范围是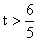 .………………………………14分
.………………………………14分


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:高中数学 来源:2012-2013安徽省高二下学期第二次5月质量检测理科数学卷(解析版) 题型:解答题
已知函数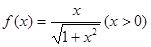 ,数列
,数列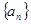 满足
满足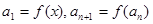 。
。
(1)求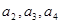 ;
;
(2)猜想数列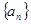 的通项公式,并用数学归纳法予以证明。
的通项公式,并用数学归纳法予以证明。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省高三第五次月考文科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知函数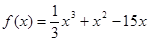 ,数列
,数列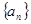 满足
满足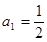 ,
,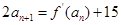 ;数列
;数列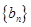 的前
的前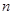 项和为
项和为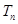 ,数列
,数列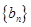 的前
的前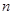 项积为
项积为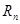 ,
,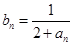
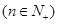 .
.
(1)求证: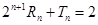 ;
;
(2)求证: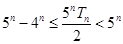 .
.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省连州市高三8月月考理科数学试卷(解析版) 题型:解答题
已知函数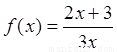 ,数列
,数列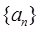 满足
满足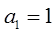 ,
,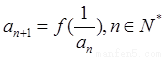 .
.
(1)求数列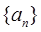 的通项公式;
的通项公式;
(2)令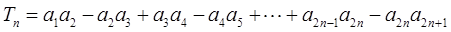 ,求
,求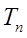 ;
;
(3)令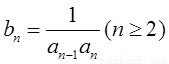 ,
,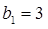 ,
,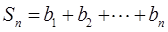 ,若
,若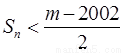 对一切
对一切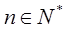 成立,求最小正整数
成立,求最小正整数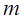 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省珠海市高三入学摸底考试理科数学卷 题型:解答题
(本小题满分14分)
已知函数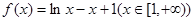 ,数列
,数列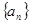 满足
满足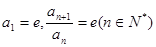 .
.
(Ⅰ)求数列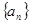 的通项公式
的通项公式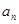 ;
;
(Ⅱ)求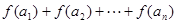 ;
;
(Ⅲ)求证: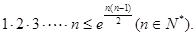
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com