
【题目】如图,有一边长为6的正方形铁片,在铁片的四角各截去一个边长为x的小正方形后,沿图中虚线部分折起,做成一个无盖方盒. 
(1)试用x表示方盒的容积V(x),并写出x的范围;
(2)求方盒容积V(x)的最大值及相应x的值.
【答案】
(1)解:由题意,无盖方盒底面是边长为6﹣2x的正方形,高为x,
从而有:V(x)=x(6﹣2x)2=4x3﹣24x2+36x,
其中,x满足: ![]() ,∴0<x<3
,∴0<x<3
(2)解:由(1)知:V(x)=4x3﹣24x2+36x,x∈(0,3),
V′(x)=12x2﹣48x+36=12(x﹣1)(x﹣3),
若0<x<1,则V′(x)>0;若1<x<3,则V′(x)<0,
∴V(x)在(0,1)上单调递增,在(1,3)上单调递减,
∴V(x)在x=1处取得极大值,也是最大值,
∴V(x)max=V(1)=16,
故方盒容积V(x)的最大值为16,相应x的值为1
【解析】(1)求出方盒的容积V(x),根据边长大于0,求出x的范围即可;(2)求出v(x)的导数,根据函数的单调性求出v(x)的最大值以及相应x的值即可.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱 ![]() 中,点E,F分别是棱CC1 , BB1上的点,点M是线段AC上的动点,EC=2FB=2,若MB∥平面AEF,试判断点M的位置.
中,点E,F分别是棱CC1 , BB1上的点,点M是线段AC上的动点,EC=2FB=2,若MB∥平面AEF,试判断点M的位置.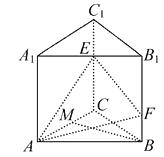
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求倾斜角为直线y= ![]() +1的倾斜角的一半,且分别满足下列条件的直线方程:(1)
+1的倾斜角的一半,且分别满足下列条件的直线方程:(1)
【答案】解:∵直线l1:y= ![]() +1的斜率k1=
+1的斜率k1= ![]() ,
,
∴直线l1的倾斜角为120°,∴所求直线的倾斜角为60°,斜率k= ![]() .
.
∵过点(-4,1),∴直线方程为y-1= ![]() (x+4)
(x+4)
(1)经过点(-4,1)
(2)在y轴上的截距为-10.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:|x﹣a|<3(a为常数);q:代数式 ![]() 有意义.
有意义.
(1)若a=1,求使“p∧q”为真命题的实数x的取值范围;
(2)若p是q成立的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+(x﹣c)|x﹣c|,a<0,c>0 (Ⅰ)当 ![]() 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(Ⅱ)设函数f(x)的图象在点P(x1 , f(x1)),Q(x2 , f(x2))两处的切线分别为l1 , l2 . 若 ![]() ,且l1⊥l2 , 求实数c的最小值.
,且l1⊥l2 , 求实数c的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某产品出厂前需要依次通过三道严格的审核程序,三道审核程序通过的概率依次为 ![]() ,
, ![]() ,
, ![]() ,每道程序是相互独立的,且一旦审核不通过就停止审核,该产品只有三道程序都通过才能出厂销售 (Ⅰ)求审核过程中只通过两道程序的概率;
,每道程序是相互独立的,且一旦审核不通过就停止审核,该产品只有三道程序都通过才能出厂销售 (Ⅰ)求审核过程中只通过两道程序的概率;
(Ⅱ)现有3件该产品进入审核,记这3件产品可以出厂销售的件数为X,求X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com