
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
分析 由题意画出图形,结合图形逐一分析三个命题得答案.
解答 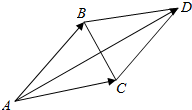 解:如图,在△ABC中,∵AB=AC,
解:如图,在△ABC中,∵AB=AC,
∴△ABC为等腰三角形,
又2$\overrightarrow{AP}$=($\overrightarrow{AB}$+$\overrightarrow{AC}$),
∴P为底边BC的中点.
则①$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$,正确;
②$\overrightarrow{PA}$•($\overrightarrow{AC}$-$\overrightarrow{AB}$)=$\overrightarrow{PA}•\overrightarrow{BC}=0$,正确;
③四边形ABDC为菱形,直线AP平分∠A,正确.
故选:D.
点评 本题考查命题的真假判断与应用,考查了平面向量的数量积运算,考查向量的加法法则,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
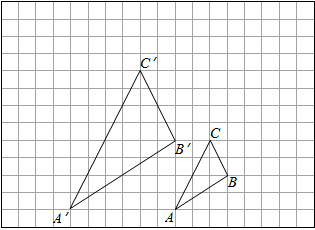 如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com