
【题目】若关于x的不等式(ax+1)(ex﹣aex)≥0在(0,+∞)上恒成立,则实数a的取值范围是( )
A.(﹣∞,1]
B.[0,1]
C.![]()
D.[0,e]
【答案】B
【解析】解:∵不等式(ax+1)(ex﹣aex)≥0在(0,+∞)上恒成立, ∴①当a=0时,(ax+1)(ex﹣aex)=ex>0在(0,+∞)上恒成立;
②当a<0时,ex﹣aex>0恒成立,故不等式(ax+1)(ex﹣aex)≥0在(0,+∞)上恒成立
ax+1≥0在(0,+∞)上恒成立a≥﹣ ![]() 在(0,+∞)上恒成立.
在(0,+∞)上恒成立.
∵y=﹣ ![]() 在(0,+∞)上单调递增,
在(0,+∞)上单调递增,
∴当x→+∞时,y→0,
∴a≥0,又a<0,∴a∈;
③当a>0时,ax+1>0恒成立,故不等式(ax+1)(ex﹣aex)≥0在(0,+∞)上恒成立
ex﹣aex≥0在(0,+∞)上恒成立a≤ ![]() 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,
因此,a≤( ![]() )min ,
)min ,
令g(x)= ![]() (x>0),则g′(x)=
(x>0),则g′(x)= ![]() =
= ![]() (x>0),
(x>0),
当0<x<1时,g′(x)<0,g(x)在区间(0,1)上单调递减;
当x>1时,g′(x)>0,g(x)在区间(1,+∞)上单调递增;
∴当x=1时,g(x)= ![]() (x>0)取得极小值g(1)=1,也是最小值,
(x>0)取得极小值g(1)=1,也是最小值,
∴0<a≤1,
综上所述,0≤a≤1,
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC-A′B′C′,底面是边长为1的正三角形,侧面为全等的矩形且高为8,求一点自A点出发沿着三棱柱的侧面绕行一周后到达A′点的最短路线长.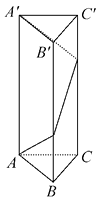
本题条件不变,求一点自A点出发沿着三棱柱的侧面绕行两周后到达A′点的最短路线长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二手车经销商小王对其所经营的某一型号二手汽车的使用年数x(0<x≤10)与销售价格y(单位:万元/辆)进行整理,得到如表的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(1)试求y关于x的回归直线方程;(参考公式: ![]() =
= 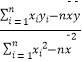 ,
, ![]() =y﹣
=y﹣ ![]() )
)
(2)已知每辆该型号汽车的收购价格为w=0.01x3﹣0.09x2﹣1.45x+17.2万元,根据(1)中所求的回归方程,预测x为何值时,小王销售一辆该型号汽车所获得的利润L(x)最大?(利润=售价﹣收购价)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且a1=1,an+1=2Sn+1,数列{bn}满足a1=b1 , 点P(bn , bn+1)在直线x﹣y+2=0上,n∈N* .
(1)求数列{an},{bn}的通项公式;
(2)设 ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一元二次不等式f(x)<0的解集为{x|x<﹣1或 ![]() ,则f(ex)>0的解集为( )
,则f(ex)>0的解集为( )
A.{x|x<﹣1或x>﹣ln3}
B.{x|﹣1<x<﹣ln3}
C.{x|x>﹣ln3}
D.{x|x<﹣ln3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂拟生产甲、乙两种适销产品,每件产品甲的销售收入为3千元,每件产品乙的销售收入为4千元.这两种产品都需要在A,B两种不同的设备上加工,按工艺规定,一件产品甲和一件产品乙在各设备上需要加工工时如表所示:
设备 | A | B |
甲 | 2h | 1h |
乙 | 2h | 2h |
已知A,B两种设备每月有效使用台时数分别为400h、300h(一台设备工作一小时称为一台时).分别用x,y表示计划每月生产甲、乙产品的件数.
(Ⅰ)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问每月分别生产甲、乙两种产品各多少件,可使每月的收入最大?并求出此最大收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos22x﹣2,给出下列命题:
①β∈R,f(x+β)为奇函数;
②α∈(0, ![]() ),f(x)=f(x+2α)对x∈R恒成立;
),f(x)=f(x+2α)对x∈R恒成立;
③x1 , x2∈R,若|f(x1)﹣f(x2)|=2,则|x1﹣x2|的最小值为 ![]() ;
;
④x1 , x2∈R,若f(x1)=f(x2)=0,则x1﹣x2=kπ(k∈Z).其中的真命题有( )
A.①②
B.③④
C.②③
D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com