
【题目】已知函数 ![]() ,x∈R,ω>0.
,x∈R,ω>0.
(1)求函数f(x)的值域;
(2)若函数y=f(x)的图象与直线y=﹣1的两个相邻交点间的距离为 ![]() ,求函数y=f(x)的单调区间.
,求函数y=f(x)的单调区间.
【答案】
(1)解:∵f(x)=函数 ![]() ,
,
=( ![]() )+(
)+( ![]() )﹣(cosωx+1),
)﹣(cosωx+1),
= ![]() …(4分),
…(4分),
∵x∈R,
∴ ![]() ,
,
∴ ![]() ,
,
∴函数y=f(x)的值域为[﹣3,1]
(2)解:∵由题设条件和三角函数图象和性质知:
函数y=f(x)的周期为π,
∴ ![]() ,
,
∴ ![]() ,
,
![]() ,
,
![]() ,
,
∴ ![]()
【解析】(1)根据凑角公式整理已知函数式转化为单一的三角函数,借助三角函数的值域得到结论。(2)由题设条件以及三角函数的图像和性质可得y=f(x)的周期为π,进而求出![]() 故得到f ( x )的解析式,再根据正弦函数的单调性由整体思想即可得出结果。
故得到f ( x )的解析式,再根据正弦函数的单调性由整体思想即可得出结果。
【考点精析】利用函数y=Asin(ωx+φ)的图象变换对题目进行判断即可得到答案,需要熟知图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( ) 
A.小球第10次着地时向下的运动共经过的路程
B.小球第11次着地时向下的运动共经过的路程
C.小球第10次着地时一共经过的路程
D.小球第11次着地时一共经过的路程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 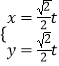 (t为参数),圆C的方程为x2+y2﹣4x﹣2y+4=0.以O为极点,x轴正半轴为极轴建立极坐标系.
(t为参数),圆C的方程为x2+y2﹣4x﹣2y+4=0.以O为极点,x轴正半轴为极轴建立极坐标系.
(1)求l的普通方程与C的极坐标方程;
(2)已知l与C交于P,Q,求|PQ|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2+ax﹣a)e1﹣x , 其中a∈R. (Ⅰ)求函数f'(x)的零点个数;
(Ⅱ)证明:a≥0是函数f(x)存在最小值的充分而不必要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,PC⊥平面ABCD,点E在棱PA上. 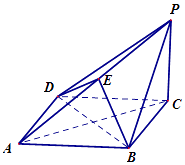
(Ⅰ)求证:直线BD⊥平面PAC;
(Ⅱ)若PC∥平面BDE,求证:AE=EP;
(Ⅲ)是否存在点E,使得四面体A﹣BDE的体积等于四面体P﹣BDC的体积的 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x的图象向左平移 ![]() 个单位后,得到函数y=g(x)的图象,下列关于y=g(x)的说法正确的是( )
个单位后,得到函数y=g(x)的图象,下列关于y=g(x)的说法正确的是( )
A.图象关于点(﹣ ![]() ,0)中心对称
,0)中心对称
B.图象关于x=﹣ ![]() 轴对称
轴对称
C.图象关于点(﹣ ![]() ,0)中心对称
,0)中心对称
D.图象关于x=﹣ ![]() 轴对称
轴对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+ ![]() (a≠0).
(a≠0).
(1)若a=1,解关于x的不等式f(x)≥|x﹣2|;
(2)若不等式f(x)﹣f(x+m)≤1恒成立,求正数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥P﹣ABC的各顶点都在同一球的面上,且PA⊥平面ABC,若球O的体积为 ![]() (球的体积公式为
(球的体积公式为 ![]() R3 , 其中R为球的半径),AB=2,AC=1,∠BAC=60°,则三棱锥P﹣ABC的体积为( )
R3 , 其中R为球的半径),AB=2,AC=1,∠BAC=60°,则三棱锥P﹣ABC的体积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com