
【题目】在如图所示的四棱锥P﹣ABCD中,四边形ABCD为正方形,PA⊥CD,BC⊥平面PAB,且E,M,N分别为PD,CD,AD的中点, ![]() =3
=3 ![]() .
. 
(1)证明:PB∥平面FMN;
(2)若PA=AB,求二面角E﹣AC﹣B的余弦值. 
【答案】
(1)证明:连结BD,分别交AC、MN于点O,G,连结EO、FG,
∵O为BD中点,E为PD中点,∴EO∥PB,
又 ![]() =3
=3 ![]() ,∴F为ED中点,又CM=MD,AN=DN,∴G为OD的中点,
,∴F为ED中点,又CM=MD,AN=DN,∴G为OD的中点,
∴FG∥EO,∴PB∥FG,
∵FG平面FMN,PB平面FMN,
∴PB∥平面FMN.
(2)解:∵BC⊥平面PAB,∴BC⊥PA,又PA⊥CD,BC∩CD=C,
∴PA⊥平面ABCD,
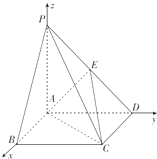
如图,以A为坐标原点,AB,AD,AP所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,
设PA=AB=2,则A(0,0,0),B(2,0,0),C(2,2,0),E(0,1,1),
则 ![]() =(2,2,0),
=(2,2,0), ![]() =(0,1,1),
=(0,1,1),
平面ABCD的一个向向量 ![]() =(0,0,1),
=(0,0,1),
设平面AEC的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 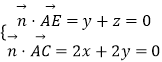 ,取x=1,得
,取x=1,得 ![]() =(1,﹣1,1),
=(1,﹣1,1),
∴cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() ,
,
由图知二面角E﹣AC﹣B为钝角,
∴二面角E﹣AC﹣B的余弦值为﹣ ![]() .
.
【解析】(1)连结BD,分别交AC、MN于点O,G,连结EO、FG,推导出EO∥PB,FG∥EO,PB∥FG,由此能证明PB∥平面FMN.(2)以A为坐标原点,AB,AD,AP所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,由此能求出二面角E﹣AC﹣B的余弦值.
【考点精析】关于本题考查的直线与平面平行的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为 ![]() (α为参数)以原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为
(α为参数)以原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为 ![]() .若直线l与曲线C交于A,B,求线段AB的长.
.若直线l与曲线C交于A,B,求线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈[-1,2],函数f(x)=x2-x的值大于0,若p∨q是真命题,则命题q可以是( )
A. x0∈(-1,1),cos x0<![]()
B. “-3<m<0”是“函数f(x)=x+log2x+m在区间![]() 上有零点”的必要不充分条件
上有零点”的必要不充分条件
C. x=![]() 是曲线f(x)=
是曲线f(x)=![]() sin 2x+cos 2x的一条对称轴
sin 2x+cos 2x的一条对称轴
D. 若x∈(0,2),则在曲线f(x)=ex(x-2)上任意一点处的切线的斜率不小于![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+ ![]() )(ω>0)的最小正周期为π,则该函数的图象( )
)(ω>0)的最小正周期为π,则该函数的图象( )
A.关于直线x= ![]() 对称
对称
B.关于点( ![]() ,0)对称
,0)对称
C.关于直线x=﹣ ![]() 对称
对称
D.关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣a(x﹣1),g(x)=ex .
(1)当a=2时,求函数f(x)的最值;
(2)当a≠0时,过原点分别作曲线y=f(x)与y=g(x)的切线l1 , l2 , 已知两切线的斜率互为倒数,证明: ![]() <a<
<a< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网上购物系统是一种具有交互功能的商业信息系统,它在网络上建立一个虚拟的购物商场,使购物过程变得轻松、快捷、方便.网上购物系统分为前台管理和后台管理,前台管理包括浏览商品、查询商品、订购商品、用户注册等功能;后台管理包括公告管理、商品管理、订单管理、投诉管理和用户管理等模块.根据这些要求画出该系统的结构图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆C的方程为ρ=2acosθ(a≠0),以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系,设直线l的参数方程为 ![]() (t为参数).
(t为参数).
(1)求圆C的直角坐标方程(化为标准方程)和直线l的极坐标方程;
(2)若直线l与圆C只有一个公共点,且a<1,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市化工厂三个车间共有工人1 000名,各车间男、女工人数如下表:
第一车间 | 第二车间 | 第三车间 | |
女工 | 173 | 100 | y |
男工 | 177 | x | z |
已知在全厂工人中随机抽取1名,抽到第二车间男工的可能性是0. 15.
(1)求x的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com