
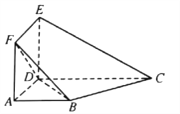
【题目】如图,某几何体![]() 中,四边形
中,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形, ![]() 是直角梯形,
是直角梯形, ![]() 是直角,
是直角, ![]() ,
, ![]() 是以
是以![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形, ![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析: ![]() 因为
因为![]() ,
, ![]() ,可证
,可证![]() 平面
平面![]() ,从而证明平面
,从而证明平面![]() 平面
平面![]() ;
; ![]() 由
由![]() 得到
得到![]() ,又因为四边形
,又因为四边形![]() 为正方形,所以
为正方形,所以![]() 又
又![]() ,以
,以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 所在直线分别为
所在直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,求出平面
,求出平面![]() 与平面
与平面![]() 的法向量,将求二面角问题转化为求两向量夹角。
的法向量,将求二面角问题转化为求两向量夹角。
解析:(1)因为![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,故
,故![]() .
.
而四边形![]() 为正方形,所以
为正方形,所以![]() 又
又![]() ,
,
以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 所在直线分别为
所在直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .
.
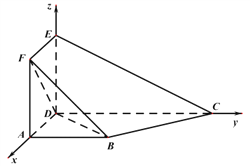
依题意易知: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() ,即
,即![]() ,令
,令![]() ,则
,则![]() ,所以
,所以![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() ,即
,即![]() ,令
,令![]() ,则
,则![]() ,所以
,所以![]() .
.
设平面![]() 与平面
与平面![]() 所成的锐二面角的平面角为
所成的锐二面角的平面角为![]() ,
,
则![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() :
: ![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求出曲线![]() 、
、![]() 的参数方程;
的参数方程;
(Ⅱ)若![]() 、
、![]() 分别是曲线
分别是曲线![]() 、
、![]() 上的动点,求
上的动点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
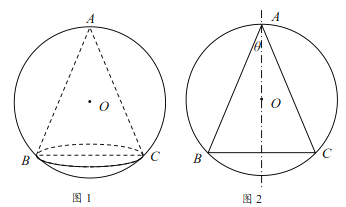
【题目】某艺术品公司欲生产一款迎新春工艺礼品,该礼品是由玻璃球面和该球的内接圆锥组成,圆锥的侧面用于艺术装饰,如图1.为了便于设计,可将该礼品看成是由圆![]() 及其内接等腰三角形
及其内接等腰三角形![]() 绕底边
绕底边![]() 上的高所在直线
上的高所在直线![]() 旋转180°而成,如图2.已知圆
旋转180°而成,如图2.已知圆![]() 的半径为
的半径为![]() ,设
,设![]() ,圆锥的侧面积为
,圆锥的侧面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)为了达到最佳观赏效果,要求圆锥的侧面积![]() 最大.求
最大.求![]() 取得最大值时腰
取得最大值时腰![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
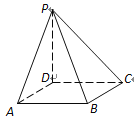
【题目】在四棱锥P–ABCD中,底面ABCD是边长为6的正方形,PD平面ABCD,PD=8.
(1) 求PB与平面ABCD所成角的大小;
(2) 求异面直线PB与DC所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() 这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.
这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.

在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,已知 ,
,已知 ,![]() .
.
(1)求![]() ;
;
(2)如图,![]() 为边
为边![]() 上一点,
上一点,![]() ,求
,求![]() 的面积
的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,长半轴长为短轴长的b倍,A,B分别为椭圆C的上、下顶点,点
,长半轴长为短轴长的b倍,A,B分别为椭圆C的上、下顶点,点![]() .
.
![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 若直线MA,MB与椭圆C的另一交点分别为P,Q,证明:直线PQ过定点.
若直线MA,MB与椭圆C的另一交点分别为P,Q,证明:直线PQ过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一款击鼓小游戏的规则如下:每轮游戏都需击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每轮游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得-200分).设每次击鼓出现音乐的概率为![]() ,且各次击鼓是否出现音乐相互独立.
,且各次击鼓是否出现音乐相互独立.
(1)玩三轮游戏,至少有一轮出现音乐的概率是多少?
(2)设每轮游戏获得的分数为X,求X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com