
 ,求实数m的取值范围.
,求实数m的取值范围.
 得,y2-2pky-2pm=0,再由韦达定理能够导出抛物线方程;
得,y2-2pky-2pm=0,再由韦达定理能够导出抛物线方程; =
= ,能够导出△AOB面积的最小值;
,能够导出△AOB面积的最小值; =
=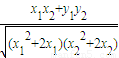 =
=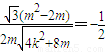 ,由此能求出实数m的取值范围.
,由此能求出实数m的取值范围.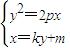 得,y2-2pky-2pm=0,
得,y2-2pky-2pm=0, ,
,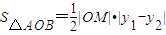

 =m
=m .
.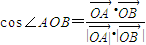 =
=
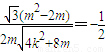 ,
,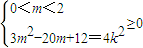 ,
, .
.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
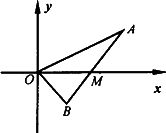
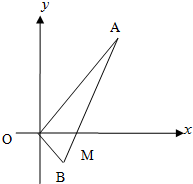 如图,线段AB过x轴正半轴上一点M(m,0)(m>0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线.
如图,线段AB过x轴正半轴上一点M(m,0)(m>0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线.| 2π | 3 |
查看答案和解析>>
科目:高中数学 来源:江西省德兴一中2011-2012学年高二下学期第一次月考数学理科试题 题型:044
如图,线段AB过x轴正半轴上一定点M(m,0),端点A、B到x轴的距离之积为2 m,以x轴为对称轴,过A、O、B三点作抛物线,求该抛物线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年洛阳市统一考试理)(12分) 如图,线段AB 过x轴的正半轴上一点M(m,0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线
(1)求抛物线方程
(2)若tan∠AOB=-1,求m的最大值

查看答案和解析>>
科目:高中数学 来源:2013届江西省高二第二学期第一次月考理科数学 题型:解答题
(12分)如图,线段AB过x轴正半轴上一定点M(m,0),端点A、B到x轴的距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线,求该抛物线的方程。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com