
(本小题满分16分)数列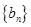
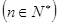 是递增的等比数列,且
是递增的等比数列,且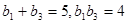 .
.
(1)求数列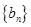 的通项公式;
的通项公式;
(2)若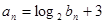 ,求证数列
,求证数列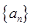 是等差数列;
是等差数列;
(3)若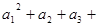 ……
……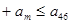 ,求
,求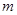 的最大值.
的最大值.
(Ⅰ)等比数列{bn}的公比为 ,
, ;(Ⅱ)见解析;
;(Ⅱ)见解析;
(Ⅲ)最大值是7.
解析试题分析: (1)根据韦达定理得到数列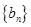 的首项和第三项,进而得到其通项公式。
的首项和第三项,进而得到其通项公式。
(2)在第一问的基础上,可知得到数列an的通项公式,运用定义证明。
(3)根据数列的前n项和得到数列的和式,求解m的范围。
解:(Ⅰ)由 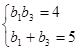 知
知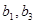 是方程
是方程 的两根,
的两根,
注意到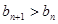 得
得 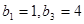 .……2分
.……2分 
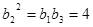 得
得 .
.
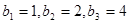
 等比数列{bn}的公比为
等比数列{bn}的公比为 ,
, ……………………6分
……………………6分
(Ⅱ)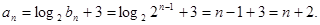 …………9分
…………9分
∵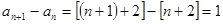
 数列{an}是首项为3,公差为1的等差数列. …………………………11分
数列{an}是首项为3,公差为1的等差数列. …………………………11分
(Ⅲ) 由(Ⅱ)知数列{an}是首项为3,公差为1的等差数列,有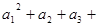 ……
……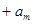 =
=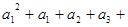 ……
……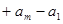
=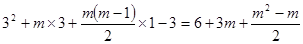 …………………………13分
…………………………13分
∵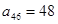

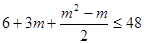 ,整理得
,整理得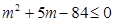 ,
,
解得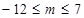 .
.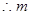 的最大值是7. …………16分.
的最大值是7. …………16分.
考点:本题主要考查了等差数列与的等比数列的前n项和与通项公式的运用。
点评:解决该试题的关键是根据韦达定理来求解得到数列bn的首项与第三项的值。进而得到数列的an的通项公式。进而根据前n项和得到数列的求和。


 天天向上口算本系列答案
天天向上口算本系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com