
【题目】算法如图,若输入m=210,n=117,则输出的n为( ) 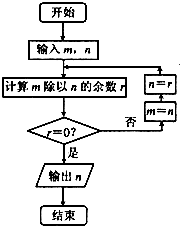
A.2
B.3
C.7
D.11
科目:高中数学 来源: 题型:
【题目】某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)[90,100]后,画出如下部分频率分布直方图.观察图形的信息,回答下列问题: 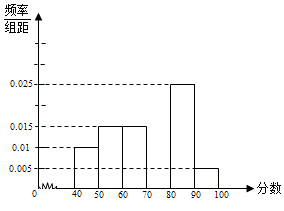
(Ⅰ) 求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 设学生甲、乙的成绩属于区间[40,50),现从成绩属于该区间的学生中任选两人,求甲、乙中至少有一人被选的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公比为正数的等比数列{an}(n∈N*),首项a1=3,前n项和为Sn , 且S3+a3、S5+a5、S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)设bn= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:kx﹣y+1+2k=0(k∈R) (Ⅰ)证明直线l经过定点并求此点的坐标;
(Ⅱ)若直线l不经过第四象限,求k的取值范围;
(Ⅲ)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.
,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N. 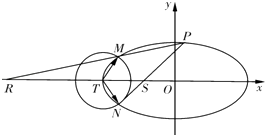
(1)求椭圆C的方程;
(2)求 ![]() 的最小值,并求此时圆T的方程;
的最小值,并求此时圆T的方程;
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:|OR||OS|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论:
①方程k= ![]() 与方程y-2=k(x+1)可表示同一直线;
与方程y-2=k(x+1)可表示同一直线;
②直线l过点P(x1 , y1),倾斜角为 ![]() ,则其方程为x=x1;
,则其方程为x=x1;
③直线l过点P(x1 , y1),斜率为0,则其方程为y=y1;
④所有直线都有点斜式和斜截式方程.
其中正确的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com