
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,经过椭圆
,经过椭圆![]() 的右焦点的弦中最短弦长为2.
的右焦点的弦中最短弦长为2.
(1)求椭圆的![]() 的方程;
的方程;
(2)已知椭圆![]() 的左顶点为
的左顶点为![]() 为坐标原点,以
为坐标原点,以![]() 为直径的圆上是否存在一条切线
为直径的圆上是否存在一条切线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() ,且直线
,且直线![]() 与
与![]() 的斜率的乘积为
的斜率的乘积为![]() ?若存在,求切线
?若存在,求切线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
【题目】某企业生产一种机器的固定成本(即固定投入)为0.5万元,但每生产100台时,又需可变成本(即另增加投入)0.25万元.市场对此商品的年需求量为500台,销售的收入(单位:万元)函数为![]() ,其中
,其中![]() 是产品生产的数量(单位:百台).
是产品生产的数量(单位:百台).
(1)求利润关于产量的函数.
(2)年产量是多少时,企业所得的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定函数![]() 和常数
和常数![]() ,若
,若![]() 恒成立,则称(
恒成立,则称(![]() )为函数
)为函数![]() 的一个“好数对”,已知函数
的一个“好数对”,已知函数![]() 的定义域为
的定义域为![]() .
.
(1)若(1,1)是函数![]() 的一个“好数对”,且
的一个“好数对”,且![]() ,求
,求![]() ,
,![]() ;
;
(2)若(2,0)是函数![]() 的一个“好数对”,且当
的一个“好数对”,且当![]() 时,
时,![]() ,判断方程
,判断方程![]() 在区间[1,8]上根的个数;
在区间[1,8]上根的个数;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》里有一段叙述:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增十三里;驽马初日行九十七里,日减半里;良马先至齐,复还迎驽马,二马相逢.根据该问题设计程序框图如下,若输入![]() ,则输出
,则输出![]() 的值是( )
的值是( )
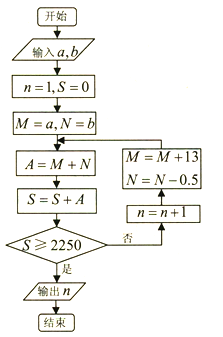
A. 8 B. 9 C. 12 D. 16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其左、右焦点分别为
,其左、右焦点分别为![]() ,点
,点![]() 是坐标平面内一点,且
是坐标平面内一点,且![]() ,
, ![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且斜率为
且斜率为![]() 的动直线
的动直线![]() 交椭圆于
交椭圆于![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使以
,使以![]() 为直径的圆恒过该点?若存在,求出点
为直径的圆恒过该点?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中,其中错误的个数是()
①经过球面上任意两点,可以作且只可以作一个大圆;
②经过球直径的三等分点,作垂直于该直径的两个平面,则这两个平面把球面分成三部分的面积相等;
③球的面积是它大圆面积的四倍;
④球面上两点的球面距离,是这两点所在截面圆上,以这两点为端点的劣弧的长.
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确命题的个数是
(1)对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,判断“
越小,判断“![]() 与
与![]() 有关系”的把握越大;
有关系”的把握越大;
(2)若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差不变;
(3)在残差图,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;
(4)设随机变量![]() 服从正态分布
服从正态分布![]() ;
;
若![]() ,则
,则![]() ( )
( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com