
【题目】如图(1),等腰梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 的两个三等分点.若把等腰梯形沿虚线
的两个三等分点.若把等腰梯形沿虚线![]() 、
、![]() 折起,使得点
折起,使得点![]() 和点
和点![]() 重合,记为点
重合,记为点![]() ,如图(2).
,如图(2).
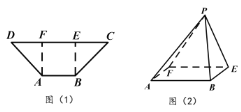
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0与1两个数字随机填入如图所示的5个格子里,每个格子填一个数字,并且从左到右数,不管数到哪个格子,总是1的个数不少于0的个数,则这样填法的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() ,
,![]() 满足下列条件:①
满足下列条件:①![]() ,
,![]() ;②当
;②当![]() 时,
时,![]() 满足:
满足:![]() 时,
时,![]() ,
,![]() ;
;![]() 时,
时,![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 和
和![]() 的值,并猜想数列
的值,并猜想数列![]() 可能的通项公式(不需证明);
可能的通项公式(不需证明);
(2)若![]() ,
,![]() ,
,![]() 是满足
是满足![]() 的最大整数,求
的最大整数,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下面几种说法:
①相等向量的坐标相同;
②若向量![]() 满足
满足![]() ,则
,则![]()
③若![]() ,
,![]() ,
,![]() ,
,![]() 是不共线的四点,则“
是不共线的四点,则“![]() ”是“四边形
”是“四边形![]() 为平行四边形”的充要条件;
为平行四边形”的充要条件;
④![]() 的充要条件是
的充要条件是![]() 且
且![]() .
.
其中正确说法的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意实数![]() ,给出下列命题:①“
,给出下列命题:①“![]() ”是“
”是“![]() ”的充要条件;②“
”的充要条件;②“![]() 是无理数”是“
是无理数”是“![]() 是无理数”的充要条件;③“
是无理数”的充要条件;③“![]() ”是“
”是“![]() ”的充分条件;④“
”的充分条件;④“![]() ”是“
”是“![]() ”的必要条件;其中真命题的个数是( )
”的必要条件;其中真命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
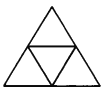
【题目】将边长为![]() 的正三角形利用平行于边的直线剖分为
的正三角形利用平行于边的直线剖分为![]() 个边长为1的小正三角形.图3为
个边长为1的小正三角形.图3为![]() 的情形.证明:存在正整数
的情形.证明:存在正整数![]() ,使得小三角形的顶点中可选出2000
,使得小三角形的顶点中可选出2000![]() 个点,其中,任意三点均不构成正三角形.
个点,其中,任意三点均不构成正三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com