
(本小题满分10分)
如图,已知三角形的顶点为A(2, 4),B(0,-2),C(-2,3),

求:
(Ⅰ)AB边上的中线CM所在直线的一般方程;
(Ⅱ)求△ABC的面积.
(1)2x+3y—5=0,(2)11。
【解析】
试题分析:(Ⅰ)因为A(2,4),B(0,-2),C-2,3),所以AB的中点M(1,1),AB边上的中线CM过点(1,1)和(-2,3),所以中线CM的斜率是k=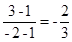 ,所以AB边上的中线CM所在直线的一般方程2x+3y—5=0。
,所以AB边上的中线CM所在直线的一般方程2x+3y—5=0。
(2))因为A(2,4),B(0,-2),C-2,3),由两点间的距离公式得:AB=2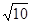 ,又AB所在直线方程为
,又AB所在直线方程为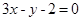 ,点C到直线AB的距离为:
,点C到直线AB的距离为: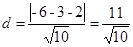 ,所以
,所以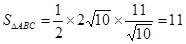 。
。
考点:直线方程的求法;两点间的距离公式;点到直线的距离公式;中点坐标公式;斜率公式。
点评:本题是一个求直线方程和三角形的面积的题目,条件给出的是点的坐标,利用代数方法来解决几何问题,这是解析几何的特点,这是一个典型的数形结合的问题。


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
|
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
查看答案和解析>>
科目:高中数学 来源: 题型:
 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com