
 的取值范围是( )
的取值范围是( )A.  | B. | C. | D. |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
 (
( 为圆柱的高,
为圆柱的高, 为球的半径,
为球的半径, ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为 千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为 千元.
千元. 关于
关于 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域; 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .
. 为常数且
为常数且
 时,求
时,求 ;
; 满足
满足 ,但
,但 ,则称
,则称 为
为 的二阶周期点.证明函数
的二阶周期点.证明函数 有且仅有两个二阶周期点,并求二阶周期点
有且仅有两个二阶周期点,并求二阶周期点 ;
; ,设
,设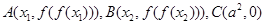 ,记
,记 的面积为
的面积为 ,求
,求 在区间
在区间 上的最大值和最小值。
上的最大值和最小值。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 上的一个映射,正整数数对
上的一个映射,正整数数对 在映射f下的象为实数z,记作
在映射f下的象为实数z,记作 . 对于任意的正整数
. 对于任意的正整数 ,映射
,映射 由下表给出:
由下表给出: |  |  |  |
 |  |  |  |
 __________,使不等式
__________,使不等式 成立的x的集合是_____________.
成立的x的集合是_____________.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 上选择一点C建造垃圾处理厂,其对市区的影响度与所选地
上选择一点C建造垃圾处理厂,其对市区的影响度与所选地  的中点时,对两市区的总影响度为0.065.
的中点时,对两市区的总影响度为0.065. 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到赤坎区的距离;若不存在,说明理由.
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到赤坎区的距离;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
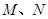 满足条件:①
满足条件:①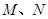 都在函数
都在函数 的图象上;②
的图象上;②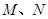 关于原点对称.则称点对
关于原点对称.则称点对 为函数
为函数 的一对“友好点对”.(注:点对
的一对“友好点对”.(注:点对 与
与 为同一“友好点对”).已知函数
为同一“友好点对”).已知函数 ,此函数的友好点对有( )
,此函数的友好点对有( )| A.0对 | B.1对 | C.2对 | D.3对 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com